【题目】已知函数f(x)=(x﹣1)2﹣ ![]() .
.
(Ⅰ)求函数的单调区间;
(Ⅱ)若函数f(x)有两个零点x1 , x2 , 证明x1+x2>2.
参考答案:
【答案】解:(Ⅰ) ![]() ,
,
f'(x)=0x=1,当x∈(﹣∞,1)时,f'(x)<0;当x∈(1,+∞)时,f'(x)>0.
所以函数f(x)在(﹣∞,1)上单调递增
(Ⅱ)证明: ![]() ,f(0)=1,不妨设x1<x2,
,f(0)=1,不妨设x1<x2,
又由(Ⅰ)可知0<x1<1,x2>1.2﹣x2<1,
又函数f(x)在(﹣∞,1)上单调递减,
所以x1+x2>2x1>2﹣x2等价于f(x1)<f(2﹣x2),
即0=f(x1)<f(2﹣x2).
又 ![]() ,而
,而 ![]() ,
,
所以 ![]()
设g(x)=xe2﹣x﹣(2﹣x)ex,则g'(x)=(1﹣x)(e2﹣x﹣ex)
当x∈(1,+∞)时g'(x)>0,而g(1)=0,故当x>1时,g(x)>0.
而 ![]() 恒成立,
恒成立,
所以当x>1时, ![]() ,
,
故x1+x2>2.
【解析】(Ⅰ)利用导函数在指定区间上的正负得到其增减性。(Ⅱ)由(Ⅰ)的结论得到x1>2﹣x2 即得于f(x1)<f(2﹣x2)求出 f ( 2 x 2 )的表达式,构造函数g(x)求导根据导函数的正负得出函数的最值,转化求解即可。
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,函数
时,函数 恰有两个不同的零点,求实数
恰有两个不同的零点,求实数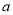 的值;
的值;(2)当
 时,
时,① 若对于任意
 ,恒有
,恒有 ,求
,求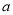 的取值范围;
的取值范围;② 若
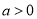 ,求函数
,求函数 在区间
在区间 上的最大值
上的最大值 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某化工厂拟建一个下部为圆柱,上部为半球的容器(如图,圆柱高为h,半径为r,不计厚度,单位:米),按计划容积为72π立方米,且h≥2r,假设其建造费用仅与表面积有关(圆柱底部不计),已知圆柱部分每平方米的费用为2千元,半球部分每平方米4千元,设该容器的建造费用为y千元.

(Ⅰ)求y关于r的函数关系,并求其定义域;
(Ⅱ)求建造费用最小时的r. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知圆M:(x+1)2+y2=
 的圆心为M,圆N:(x﹣1)2+y2=
的圆心为M,圆N:(x﹣1)2+y2=  的圆心为N,一动圆与圆M内切,与圆N外切.
的圆心为N,一动圆与圆M内切,与圆N外切.
(Ⅰ)求动圆圆心P的轨迹方程;
(Ⅱ)过点(1,0)的直线l与曲线P交于A,B两点,若 =﹣2,求直线l的方程.
=﹣2,求直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司计划在甲、乙两座城市共投资240万元,根据行业规定,每个城市至少要投资80万元,由前期市场调研可知:甲城市收益
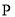 与投入
与投入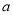 (单位:万元)满足
(单位:万元)满足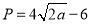 ,乙城市收益
,乙城市收益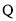 与投入
与投入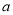 (单位:万元)满足
(单位:万元)满足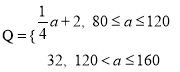 ,设甲城市的投入为
,设甲城市的投入为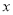 (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为 (单位:万元).
(单位:万元).(1)当投资甲城市128万元时,求此时公司总收益;
⑵试问如何安排甲、乙两个城市的投资,才能使公司总收益最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>0,b>0,且ab=1,则函数f(x)=ax与函数g(x)=﹣logbx的图象可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
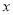 的函数
的函数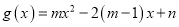 为
为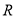 上的偶函数,且在区间
上的偶函数,且在区间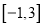 上的最大值为10. 设
上的最大值为10. 设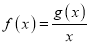 .
.⑴ 求函数
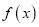 的解析式;
的解析式;⑵ 若不等式
 在
在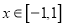 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;⑶ 是否存在实数
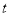 ,使得关于
,使得关于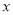 的方程
的方程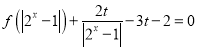 有四个不相等的实 数根?如果存在,求出实数
有四个不相等的实 数根?如果存在,求出实数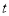 的范围,如果不存在,说明理由.
的范围,如果不存在,说明理由.
相关试题

