【题目】设函数![]() ,若
,若![]() ,使得直线
,使得直线![]() 的斜率为0,则
的斜率为0,则![]() 的最小值为( )
的最小值为( )
A. -8 B. ![]() C. -6 D. 2
C. -6 D. 2
参考答案:
【答案】C
【解析】函数f(x)=﹣x2﹣6x+m,
对称轴x=﹣3,开口向下,
当x∈[﹣5,﹣2]的值域M:f(﹣5)≤M≤f(﹣3),即m+5≤M≤9+m.
函数g(x)=2x3+3x2﹣12x﹣m,
则g′(x)=6x2+6x﹣12.
令g′(x)=0,
可得:x=﹣2或1.
当x∈(﹣∞,﹣2)和(1,+∞)时,g′(x)>0,则g(x)是递增函数.
当x∈(﹣2,1)时,g′(x)<0,则g(x)是递减函数.
∵x∈[﹣1,2]
∴g(1)min=﹣7﹣m
g(﹣1)=13﹣m,g(2)=4﹣m.
∴g(x)值域N:﹣7﹣m≤N≤13﹣m.
由题意,MN
则![]() ,
,
解得:2≥m≥﹣6.
∴m的最小值为﹣6.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 为直角梯形,
为直角梯形,  ,
,  ,平面
,平面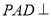 底面
底面 ,
,  为
为 的中点,
的中点,  是棱
是棱 上的点,
上的点,  ,
,  .
.
(Ⅰ)求证:平面
 平面
平面 ;
;(Ⅱ)若三棱锥
 的体积是四棱锥
的体积是四棱锥 体积的
体积的 ,设
,设 ,试确定
,试确定 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的中心在原点,一个焦点F(-2,0),且长轴长与短轴长的比为
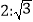 ,
,(1)求椭圆C的方程;
(2)设点M(m,0)在椭圆C的长轴上,设点P是椭圆上的任意一点,若当
 最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
 =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(
 ,
, )
)C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
-
科目: 来源: 题型:
查看答案和解析>>【题目】“双十一网购狂欢节”源于淘宝商城(天猫)2009年11月11 日举办的促销活动,当时参与的商家数量和促销力度均有限,但营业额远超预想的效果,于是11月11日成为天猫举办大规模促销活动的固定日期.如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用
 (单位:万元)和利润
(单位:万元)和利润 (单位:十万元)之间的关系,得到下列数据:
(单位:十万元)之间的关系,得到下列数据:
2
3
4
5
6
8
9
11

1
2
3
3
4
5
6
8
(1)请用相关系数
 说明
说明 与
与 之间是否存在线性相关关系(当
之间是否存在线性相关关系(当 时,说明
时,说明 与
与 之间具有线性相关关系);
之间具有线性相关关系);(2)根据(1)的判断结果,建立
 与
与 之间的回归方程,并预测当
之间的回归方程,并预测当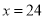 时,对应的利润
时,对应的利润 为多少(
为多少( 精确到0.1).
精确到0.1).附参考公式:回归方程中
 中
中 和
和 最小二乘估计分别为
最小二乘估计分别为 ,相关系数
,相关系数
参考数据:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况,在本市的所有中学生中随机抽取了120名学生进行调查,现将日均自学时间小于1小时的学生称为“自学不足”者
 根据调查结果统计后,得到如下
根据调查结果统计后,得到如下 列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为
列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为 .
.非自学不足
自学不足
合计
配有智能手机
30
没有智能手机
10
合计
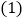 请完成上面的列联表;
请完成上面的列联表; 根据列联表的数据,能否有
根据列联表的数据,能否有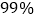 的把握认为“自学不足”与“配有智能手机”有关?
的把握认为“自学不足”与“配有智能手机”有关?附表及公式:
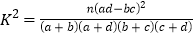 ,其中
,其中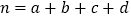
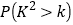
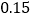
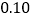
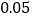
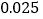
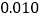
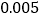
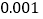
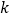
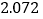
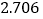
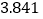
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
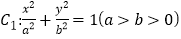 的离心率为
的离心率为 ,抛物线
,抛物线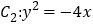 的准线被椭圆
的准线被椭圆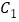 截得的线段长为
截得的线段长为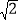 .
.(1)求椭圆
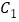 的方程;
的方程;(2)如图,点
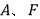 分别是椭圆
分别是椭圆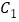 的左顶点、左焦点直线
的左顶点、左焦点直线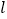 与椭圆
与椭圆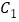 交于不同的两点
交于不同的两点 (
( 都在
都在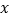 轴上方).且
轴上方).且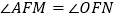 .证明:直线
.证明:直线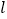 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.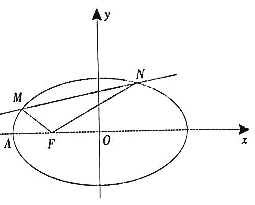
相关试题

