【题目】已知关于![]() 的函数
的函数![]() 为
为![]() 上的偶函数,且在区间
上的偶函数,且在区间![]() 上的最大值为10. 设
上的最大值为10. 设![]() .
.
⑴ 求函数![]() 的解析式;
的解析式;
⑵ 若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
⑶ 是否存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有四个不相等的实 数根?如果存在,求出实数
有四个不相等的实 数根?如果存在,求出实数![]() 的范围,如果不存在,说明理由.
的范围,如果不存在,说明理由.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)答案见解析.
;(3)答案见解析.
【解析】【试题分析】(1)利用![]() ,化简后可求得
,化简后可求得![]() .此时函数对称轴为
.此时函数对称轴为![]() 轴,故当
轴,故当![]() 时取得最大值,由此求得
时取得最大值,由此求得![]() .进而求得
.进而求得![]() .(2)将原不等式分离参数得到
.(2)将原不等式分离参数得到![]() 在
在![]() 上恒成立,利用换元法结合二次函数最值可求得
上恒成立,利用换元法结合二次函数最值可求得![]() .(3)先将原方程化为
.(3)先将原方程化为![]() .利用换元法令
.利用换元法令![]() ,将上式变为二次函数零点问题来求解.
,将上式变为二次函数零点问题来求解.
【试题解析】
(1)∵![]() 为
为![]() 上的偶函数,
上的偶函数, ![]() ,
,
![]() ,
, ![]() 关于
关于![]() 恒成立,
恒成立, ![]()
![]() ,
, ![]() 在区间
在区间![]() 上的最大值为10,
上的最大值为10,
![]() 当
当![]() 时,
时, ![]() 解得:
解得: ![]() ,
,
![]()
![]()
(2)不等式![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
上式可化为![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,∵
,∵![]() ,∴
,∴![]() ,则
,则![]() 在
在![]() 上恒成立,
上恒成立,
又∵当![]() 时,
时, ![]() ,∴
,∴![]() ,即所求实数
,即所求实数![]() 的取值范围为
的取值范围为![]()
(3)方程![]() ,即
,即![]() ,
,
可化为: ![]() ,
,
令![]() ,则
,则![]() ,
,
若关于![]() 的方程
的方程![]() 有四个不相等的实数根,
有四个不相等的实数根,
则关于![]() 的方程
的方程![]() 必须有两个不相等的实数根
必须有两个不相等的实数根![]() 和
和![]() ,
,
并且![]() ,记
,记![]()
![]() ,
,
则, 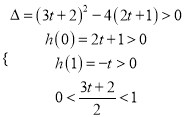
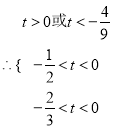 解得:
解得: ![]() ,所以,存在实数
,所以,存在实数![]() 使得关于
使得关于![]() 的方程
的方程
![]() 有四个不相等的实数根,
有四个不相等的实数根, ![]() 取值范围为
取值范围为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x﹣1)2﹣
 .
.
(Ⅰ)求函数的单调区间;
(Ⅱ)若函数f(x)有两个零点x1 , x2 , 证明x1+x2>2. -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司计划在甲、乙两座城市共投资240万元,根据行业规定,每个城市至少要投资80万元,由前期市场调研可知:甲城市收益
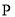 与投入
与投入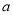 (单位:万元)满足
(单位:万元)满足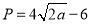 ,乙城市收益
,乙城市收益 与投入
与投入 (单位:万元)满足
(单位:万元)满足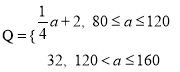 ,设甲城市的投入为
,设甲城市的投入为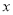 (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为 (单位:万元).
(单位:万元).(1)当投资甲城市128万元时,求此时公司总收益;
⑵试问如何安排甲、乙两个城市的投资,才能使公司总收益最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>0,b>0,且ab=1,则函数f(x)=ax与函数g(x)=﹣logbx的图象可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
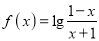 .
.(1)求不等式
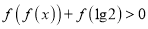 的解集;
的解集;(2)函数
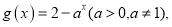 若存在
若存在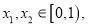 使得
使得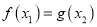 成立,求实数
成立,求实数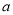 的取值范围;
的取值范围;(3)若函数
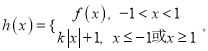 讨论函数
讨论函数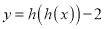 的零点个数(直接写出答案,不要求写出解题过程).
的零点个数(直接写出答案,不要求写出解题过程). -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂某种产品的年固定成本为250万元,每生产
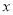 件,需另投入成本
件,需另投入成本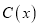 ,当年产量不足80件时,
,当年产量不足80件时, 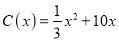 (万元),当年产量不少于80件时
(万元),当年产量不少于80件时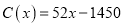 (万元),每件商品售价50万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件商品售价50万元,通过市场分析,该厂生产的商品能全部售完.(1)写出年利润
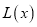 (万元)关于年产量
(万元)关于年产量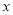 (件)的函数解析式;
(件)的函数解析式;(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点.
(1)求圆A的方程;
(2)当|MN|=2
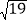 时,求直线l的方程.
时,求直线l的方程.
相关试题

