【题目】某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30分钟抽取一包产品,称其重量,分别记录抽查数据如下:
甲 | 102 | 101 | 99 | 98 | 103 | 98 | 99 |
乙 | 110 | 115 | 90 | 85 | 75 | 115 | 110 |
(1)这种抽样方法是哪一种?
(2)将两组数据用茎叶图表示.
(3)将两组数据进行比较,说明哪个车间产品较稳定.
参考答案:
【答案】解:(1)根据系统抽样的定义可知,每隔30分钟抽取一包产品,抽取的时间间隔相同,满足系统抽样的定义,
∴这种抽样方法是系统抽样.
(2)将两组数据用茎叶图表示如图:.
(3)甲的平均数为![]() (102+101+99+98+103+98+99)=100.
(102+101+99+98+103+98+99)=100.
乙的平均数为![]() (110+115+90+85+75+115+110)=100.
(110+115+90+85+75+115+110)=100.
由茎叶图中的数据可知甲的成绩主要集中在90和100附近,乙的成绩比较分散,
∴甲比乙稳定.
【解析】(1)根据抽样方法的定义进行判断.
(2)利用茎叶图的定义将两组数据用茎叶图表示.
(3)根据茎叶图中的数据的分布,即可判断两组数据的稳定性.
【考点精析】利用用样本的数字特征估计总体的数字特征对题目进行判断即可得到答案,需要熟知用样本估计总体时,如果抽样的方法比较合理,那么样本可以反映总体的信息,但从样本得到的信息会有偏差.在随机抽样中,这种偏差是不可避免的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为G(x)(万元),其中固定成本为3万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)=
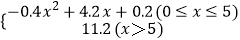 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)甲厂生产多少台新产品时,可使盈利最多? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一学生共有500人,为了了解学生的历史学习情况,随机抽取了50名学生,对他们一年来4次考试的历史平均成绩进行统计,得到频率分布直方图如图所示,后三组频数成等比数列.
(1)求第五、六组的频数,补全频率分布直方图;
(2)若每组数据用该组区间中点值(例如区间[70,80)的中点值是
75作为代表,试估计该校高一学生历史成绩的平均分;
(3)估计该校高一学生历史成绩在70~100分范围内的人数.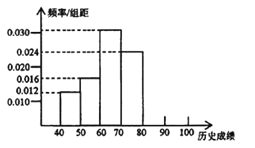
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣1|+|x+1|(x∈R)
(1)证明:函数f(x)是偶函数;
(2)利用绝对值及分段函数知识,将函数解析式写成分段函数的形式,然后画出函数图象,并写出函数的值域;
(3)在同一坐标系中画出直线y=x+2,观察图象写出不等式f(x)>x+2的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某试验田分别种植了甲乙两种水稻,为了研究这两种水稻的产量,抽检了甲、乙两种水稻的谷穗各1000株.经统计,得到每株谷穗的粒数的频率分布直方图如图:
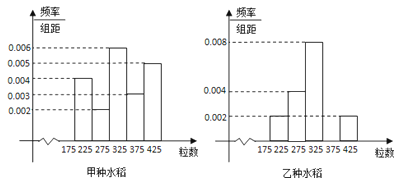
(Ⅰ)求乙种水稻谷穗的粒数落在[325,375)之间的频率,并将频率分布直方图补齐;
(Ⅱ)试根据频率分布直方图估计甲种水稻谷穗粒数的中位数与平均数(精确到0.1);
(Ⅲ)根据频率分布直方图,请至少从两方面对甲乙两种水稻谷穗的粒数作出评价. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
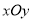 中,
中, 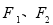 分别为椭圆
分别为椭圆 :
: 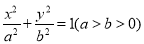 的左、右焦点,
的左、右焦点, 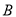 为短轴的一个端点,
为短轴的一个端点, 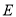 是椭圆
是椭圆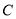 上的一点,满足
上的一点,满足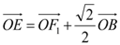 ,且
,且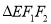 的周长为
的周长为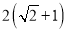 .
.(1)求椭圆
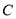 的方程;
的方程;(2)设点
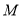 是线段
是线段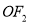 上的一点,过点
上的一点,过点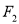 且与
且与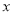 轴不垂直的直线
轴不垂直的直线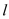 交椭圆
交椭圆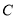 于
于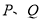 两点,若
两点,若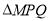 是以
是以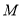 为顶点的等腰三角形,求点
为顶点的等腰三角形,求点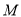 到直线
到直线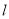 距离的取值范围.
距离的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=x2﹣mx(m>0)在区间[0,2]上的最小值记为g(m)
(1)若0<m≤4,求函数g(m)的解析式;
(2)定义在(﹣∞,0)∪(0,+∞)的函数h(x)为偶函数,且当x>0时,h(x)=g(x),若h(t)>h(4),求实数t的取值范围.
相关试题

