【题目】在平面直角坐标系![]() 中,
中, ![]() 分别为椭圆
分别为椭圆![]() :
: ![]() 的左、右焦点,
的左、右焦点, ![]() 为短轴的一个端点,
为短轴的一个端点, ![]() 是椭圆
是椭圆![]() 上的一点,满足
上的一点,满足![]() ,且
,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是线段
是线段![]() 上的一点,过点
上的一点,过点![]() 且与
且与![]() 轴不垂直的直线
轴不垂直的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,若
两点,若![]() 是以
是以![]() 为顶点的等腰三角形,求点
为顶点的等腰三角形,求点![]() 到直线
到直线![]() 距离的取值范围.
距离的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由已知![]() ,设
,设![]() ,则
,则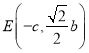 ,
, ![]() ,
, ![]() ,由此能求出椭圆
,由此能求出椭圆![]() 的方程;(2)设点
的方程;(2)设点![]() ,(
,( ![]() ),直线
),直线![]() 的方程为
的方程为![]() ,k≠0,由
,k≠0,由![]() ,得:
,得: ![]() ,由此利用韦达定理、中点坐标公式、点到直线的距离公式,结合已知条件能求出点
,由此利用韦达定理、中点坐标公式、点到直线的距离公式,结合已知条件能求出点![]() 到直线距离的取值范围.
到直线距离的取值范围.
试题解析:(1)由已知![]() ,设
,设![]() ,即
,即![]()
∴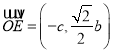 即
即 ∴
∴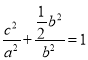 得:
得: ![]() ①
①
又![]() 的周长为
的周长为![]() ∴
∴ ![]() ②
②
又①②得: ![]() ∴
∴![]() ∴所求椭圆
∴所求椭圆![]() 的方程为:
的方程为: ![]()
(2)设点![]() ,直线
,直线![]() 的方程为
的方程为![]()
由![]() 消去
消去![]() ,得:
,得: ![]()
设![]() ,
, ![]() 中点为
中点为![]()
则![]() ∴
∴![]()
∴![]()
![]() 即
即
∵![]() 是以
是以![]() 为顶点的等腰三角形 ∴
为顶点的等腰三角形 ∴![]() 即
即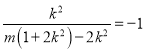
∴
设点![]() 到直线
到直线![]() 距离为
距离为![]() ,
,
则 ∴
∴![]()
即点![]() 到直线距离的取值范围是
到直线距离的取值范围是![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣1|+|x+1|(x∈R)
(1)证明:函数f(x)是偶函数;
(2)利用绝对值及分段函数知识,将函数解析式写成分段函数的形式,然后画出函数图象,并写出函数的值域;
(3)在同一坐标系中画出直线y=x+2,观察图象写出不等式f(x)>x+2的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30分钟抽取一包产品,称其重量,分别记录抽查数据如下:
甲
102
101
99
98
103
98
99
乙
110
115
90
85
75
115
110
(1)这种抽样方法是哪一种?
(2)将两组数据用茎叶图表示.
(3)将两组数据进行比较,说明哪个车间产品较稳定. -
科目: 来源: 题型:
查看答案和解析>>【题目】某试验田分别种植了甲乙两种水稻,为了研究这两种水稻的产量,抽检了甲、乙两种水稻的谷穗各1000株.经统计,得到每株谷穗的粒数的频率分布直方图如图:
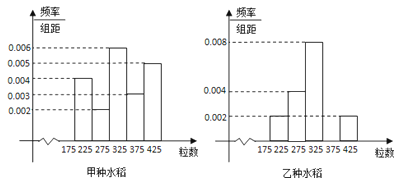
(Ⅰ)求乙种水稻谷穗的粒数落在[325,375)之间的频率,并将频率分布直方图补齐;
(Ⅱ)试根据频率分布直方图估计甲种水稻谷穗粒数的中位数与平均数(精确到0.1);
(Ⅲ)根据频率分布直方图,请至少从两方面对甲乙两种水稻谷穗的粒数作出评价. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=x2﹣mx(m>0)在区间[0,2]上的最小值记为g(m)
(1)若0<m≤4,求函数g(m)的解析式;
(2)定义在(﹣∞,0)∪(0,+∞)的函数h(x)为偶函数,且当x>0时,h(x)=g(x),若h(t)>h(4),求实数t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
: 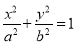 (
( )的离心率为
)的离心率为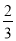 ,
,  、
、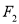 分别是它的左、右焦点,且存在直线
分别是它的左、右焦点,且存在直线 ,使
,使 、
、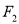 关于
关于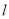 的对称点恰好是圆
的对称点恰好是圆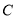 :
: 
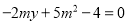 (
( ,
,  )的一条直径的两个端点.
)的一条直径的两个端点.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设直线
 与抛物线
与抛物线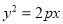 (
( )相交于
)相交于 、
、 两点,射线
两点,射线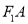 、
、 与椭圆
与椭圆 分别相交于点
分别相交于点 、
、 .试探究:是否存在数集
.试探究:是否存在数集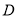 ,当且仅当
,当且仅当 时,总存在
时,总存在 ,使点
,使点 在以线段
在以线段 为直径的圆内?若存在,求出数集
为直径的圆内?若存在,求出数集 ;若不存在,请说明理由.
;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
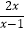 ,(x∈(﹣∞,0]∪[2,+∞))的值域为( )
,(x∈(﹣∞,0]∪[2,+∞))的值域为( )
A.[0,4]
B.[0,2)∪(2,4]
C.(﹣∞,0]∪[4,+∞)
D.(﹣∞,2)∪(2,+∞)
相关试题

