【题目】已知数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .数列
.数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() ,
, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 能否为等差数列?若能,求其通项公式;若不能,试说明理由;
能否为等差数列?若能,求其通项公式;若不能,试说明理由;
(3)若数列![]() 是各项均为正整数的递增数列,设
是各项均为正整数的递增数列,设![]() ,则当
,则当![]() ,
, ![]() ,
, ![]() 和
和![]() ,
, ![]() ,
, ![]() 均成等差数列时,求正整数
均成等差数列时,求正整数![]() ,
, ![]() ,
, ![]() 的值.
的值.
参考答案:
【答案】(1)![]() ,
, ![]() . (2)
. (2)![]() ,或
,或![]() .
.
(3)存在![]() ,
, ![]() ,
, ![]() 或
或![]() ,
, ![]() ,
, ![]() 满足条件.
满足条件.
【解析】试题分析:
(1)利用递推公式构造新数列![]() 为等比数列可求得数列的通项公式为
为等比数列可求得数列的通项公式为![]() .
.
(2)假设数列可以是等差数列,分类讨论可得![]() ,或
,或![]() .
.
(3)由题意讨论r,s,t的关系,构造函数![]() ,
,
结合函数的性质讨论可得存在![]() ,
, ![]() ,
, ![]() 或
或![]() ,
, ![]() ,
, ![]() 满足条件.
满足条件.
试题解析:
(1)由![]() ,得
,得![]() ,
,
又![]() ,所以
,所以![]() 是首项为3,公比为2的等比数列,
是首项为3,公比为2的等比数列,
则![]() ,故
,故![]() ,
, ![]() .
.
(2)由![]() ,得
,得![]() ,
,
两式相减得![]() ,即
,即![]() .①
.①
若![]() 是等差数列,设公差为
是等差数列,设公差为![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() .
.
又![]() ,即
,即![]() ,
,
解得![]() ,或
,或![]() .
.
当![]() 时,
时, ![]() ,满足条件
,满足条件![]() ;
;
当![]() 时,
时, ![]() ,也满足条件
,也满足条件![]() .
.
故![]() ,或
,或![]() .
.
(3)由![]() 是各项均为正整数的递增数列,得
是各项均为正整数的递增数列,得![]() ②,
②,
故![]() ,
, ![]() ,
,
故由①式可得![]() ,所以
,所以![]() .
.
又由①式可知![]() 是偶数,所以
是偶数,所以![]() .
.
代入①式得![]() ,所以
,所以![]() 是等差数列.
是等差数列.
由(2)知, ![]() ,
,
所以![]() .
.
若![]()
![]() ,由正整数
,由正整数![]() ,知
,知![]() ,
, ![]() .
.
当![]() 时,
时,
![]()
![]() .
.
因此要![]() 式成立,只能有
式成立,只能有![]() .
.
由![]() 式得
式得![]() ,
,
即![]() .
.
又![]() ,
, ![]() ,所以
,所以![]() ,
,
显然![]() 是方程的解.
是方程的解.
当![]() 时,设函数
时,设函数![]() ,
,
则![]() ,
,
故![]() 在
在![]() 上是增函数,所以方程
上是增函数,所以方程![]() 仅有两解
仅有两解![]() .
.
因此,存在![]() ,
, ![]() ,
, ![]() 或
或![]() ,
, ![]() ,
, ![]() 满足条件.
满足条件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,E,F是线段B1D上的两个动点,且EF=
 ,则下列结论错误的是( )
,则下列结论错误的是( ) 
A.AC⊥BF
B.直线AE,BF所成的角为定值
C.EF∥平面ABC
D.三棱锥A﹣BEF的体积为定值 -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,角
中,角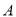 ,
, 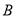 ,
, 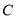 的对边分别为
的对边分别为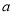 ,
, 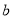 ,
, 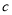 .已知
.已知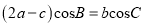 .
.(1)求角
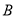 的大小;
的大小;(2)若
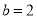 ,
, 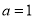 ,求
,求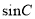 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=x2﹣4x+3,若f(x)≥mx对任意的实数x≥2都成立,则实数m的取值范围是( )
A.[﹣2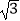 ﹣4,﹣2
﹣4,﹣2 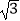 ?+4]
?+4]
B.(﹣∞,﹣2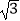 ﹣4]∪[﹣2
﹣4]∪[﹣2 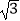 ?+4,+∞)
?+4,+∞)
C.[﹣2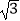 ?+4,+∞)
?+4,+∞)
D.(﹣∞,﹣ ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=logax,g(x)=loga(2x+t﹣2)2 , (a>0,a≠1,t∈R).
(1)当t=4,x∈[1,2]时F(x)=g(x)﹣f(x)有最小值为2,求a的值;
(2)当0<a<1,x∈[1,2]时,有f(x)≥g(x)恒成立,求实数t的取值范围.
(备注:函数y=x+ 在区间(0,1)上单调递减,在区间(1,+∞)上单调递增).
在区间(0,1)上单调递减,在区间(1,+∞)上单调递增). -
科目: 来源: 题型:
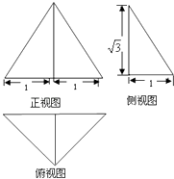
查看答案和解析>>【题目】一个简单几何体的三视图如图所示,其中正视图是一个正三角形,俯视图是等腰直角三角形,则该几何体的体积为 , 表面积为 .
-
科目: 来源: 题型:
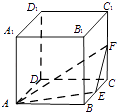
查看答案和解析>>【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段A1P长度的取值范围是 .
相关试题

