【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )(x∈R)的部分图象如图所示.
)(x∈R)的部分图象如图所示.
(Ⅰ)求函数f(x)的解析式并求函数f(x)的单调递增区间;
(Ⅱ)求函数f(x)的最小值并指出函数f(x)取最小值时相应的x的值.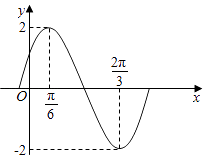
参考答案:
【答案】解:(Ⅰ)由函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )(x∈R)的部分图象可得A=2,最小正周期T=2(
)(x∈R)的部分图象可得A=2,最小正周期T=2( ![]() )=π,得ω=2,可得函数f(x)的解析式为f(x)=2sin(2x+φ),
)=π,得ω=2,可得函数f(x)的解析式为f(x)=2sin(2x+φ),
又f( ![]() )=2,
)=2,
所以sin( ![]() +φ)=1,
+φ)=1,
由于|φ|< ![]() ,可得φ=
,可得φ= ![]() ,
,
所以函数f(x)的解析式为:f(x)=2sin(2x+ ![]() )
)
由于2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,可得kπ﹣
,可得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() (k∈Z),
(k∈Z),
所以函数f(x)的单调递增区间为:[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z),
](k∈Z),
(Ⅱ)函数f(x)的最小值为﹣2,
函数f(x)取最小值﹣2时,有2x+ ![]() =2kπ﹣
=2kπ﹣ ![]() (k∈Z),可得:x=kπ﹣
(k∈Z),可得:x=kπ﹣ ![]() (k∈Z),
(k∈Z),
所以函数f(x)取最小值﹣2时相应的x的值是:x=kπ﹣ ![]() (k∈Z)
(k∈Z)
【解析】(Ⅰ)由图形可确定A,周期T,从而可得ω的值,再由f( ![]() )=2,得2×
)=2,得2× ![]() +φ=
+φ= ![]() +2kπ(k∈Z),进一步结合条件可得φ的值,即可解得f(x)的解析式,由2kπ﹣
+2kπ(k∈Z),进一步结合条件可得φ的值,即可解得f(x)的解析式,由2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,可得函数f(x)的单调递增区间;(Ⅱ)由正弦函数的图象和性质,由2x+
,可得函数f(x)的单调递增区间;(Ⅱ)由正弦函数的图象和性质,由2x+ ![]() =2kπ﹣
=2kπ﹣ ![]() (k∈Z),即可解得函数f(x)的最小值并指出函数f(x)取最小值时相应的x的值.
(k∈Z),即可解得函数f(x)的最小值并指出函数f(x)取最小值时相应的x的值.
【考点精析】关于本题考查的三角函数的最值,需要了解函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能得出正确答案.
才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在R上的偶函数,对任意x∈R,都有f(x+4π)=f(x)+f(2π)成立,那么函数f(x)可能是( )
A.f(x)=2sin x
x
B.f(x)=2cos2 x
x
C.f(x)=2cos2 x
x
D.f(x)=2cos x
x -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是( )
A.57.2,3.6
B.57.2,56.4
C.62.8,63.6
D.62.8,3.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】有下列四个说法:
①若函数f(x)=asinx+cosx(x∈R)的图象关于直线x= 对称,则a=
对称,则a= 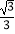 ;
;
②已知向量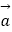 =(1,2),
=(1,2), 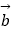 =(﹣2,m),若
=(﹣2,m),若 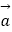 与
与 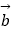 的夹角为钝角,则m<1;
的夹角为钝角,则m<1;
③当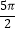 <α<
<α< 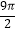 时,函数f(x)=sinx﹣logax有三个零点;
时,函数f(x)=sinx﹣logax有三个零点;
④函数f(x)=xsinx在[﹣ ,0]上单调递减,在[0,
,0]上单调递减,在[0,  ]上单调递增.
]上单调递增.
其中正确的是(填上所有正确说法的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin2
 +
+  sinωx﹣
sinωx﹣  (ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
(ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
A.(0, ]
]
B.(0, ]∪[
]∪[  ,1)
,1)
C.(0, ]
]
D.(0, ]∪[
]∪[  ,
,  ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中,  .
.(1)若
 是
是 的中点,求证:
的中点,求证:  平面
平面 ;
;(2)若
 ,求证:平面
,求证:平面 平面
平面 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
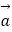 =(cosx,cosx),
=(cosx,cosx), 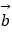 =(sinx,﹣cosx),记函数f(x)=2
=(sinx,﹣cosx),记函数f(x)=2 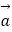
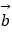 +1,其中x∈R.
+1,其中x∈R.
(Ⅰ)求函数f(x)的最小正周期及函数f(x)的图象的对称中心的坐标;
(Ⅱ)若α∈(0, ),且f(
),且f(  )=
)=  ,求cos2α的值.
,求cos2α的值.
相关试题

