【题目】有下列四个说法:
①若函数f(x)=asinx+cosx(x∈R)的图象关于直线x= ![]() 对称,则a=
对称,则a= ![]() ;
;
②已知向量 ![]() =(1,2),
=(1,2), ![]() =(﹣2,m),若
=(﹣2,m),若 ![]() 与
与 ![]() 的夹角为钝角,则m<1;
的夹角为钝角,则m<1;
③当 ![]() <α<
<α< ![]() 时,函数f(x)=sinx﹣logax有三个零点;
时,函数f(x)=sinx﹣logax有三个零点;
④函数f(x)=xsinx在[﹣ ![]() ,0]上单调递减,在[0,
,0]上单调递减,在[0, ![]() ]上单调递增.
]上单调递增.
其中正确的是(填上所有正确说法的序号)
参考答案:
【答案】①④
【解析】解:①函数f(x)=asinx+cosx= ![]() sin(x+θ),其中tanθ=
sin(x+θ),其中tanθ= ![]() ,∵其图象关于直线x=
,∵其图象关于直线x= ![]() 对称,∴θ+
对称,∴θ+ ![]() =kπ+
=kπ+ ![]() ,k∈Z,∴θ=kπ+
,k∈Z,∴θ=kπ+ ![]() ,k∈Z,∴tanθ=tan(kπ+
,k∈Z,∴tanθ=tan(kπ+ ![]() )=tan
)=tan ![]() =
= ![]() =
= ![]() ,∴a=
,∴a= ![]() ,正确;
,正确;
②已知向量 ![]() =(1,2),
=(1,2), ![]() =(﹣2,m),
=(﹣2,m), ![]() 与
与 ![]() 的夹角为钝角,则
的夹角为钝角,则 ![]() ,∴m<1且m≠﹣4,不正确;
,∴m<1且m≠﹣4,不正确;
③当 ![]() <α<
<α< ![]() 时,a可以是负数,故函数f(x)=sinx﹣logax有三个零点不正确;
时,a可以是负数,故函数f(x)=sinx﹣logax有三个零点不正确;
④f′(x)=sinx+cosxx,f′(0)=0,当x∈[0, ![]() ]时,f′(x)≥0,f(x)单调递增;当x∈[﹣
]时,f′(x)≥0,f(x)单调递增;当x∈[﹣ ![]() ,0]时,f′(x)≤0,f(x)单调递减,故正确.
,0]时,f′(x)≤0,f(x)单调递减,故正确.
所以答案是:①④.
【考点精析】关于本题考查的命题的真假判断与应用,需要了解两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】园林管理处拟在公园某区域规划建设一半径为
 米圆心角为
米圆心角为 (弧度)的扇形景观水池,其中
(弧度)的扇形景观水池,其中 为扇形
为扇形 的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过
的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过 万元,水池造价为每平方米
万元,水池造价为每平方米 元,步道造价为每米
元,步道造价为每米 元.
元.(1)当
 和
和 分别为多少时,可使广场面积最大,并求出最大值;
分别为多少时,可使广场面积最大,并求出最大值;(2)若要求步道长为
 米,则可设计出水池最大面积是多少.
米,则可设计出水池最大面积是多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在R上的偶函数,对任意x∈R,都有f(x+4π)=f(x)+f(2π)成立,那么函数f(x)可能是( )
A.f(x)=2sin x
x
B.f(x)=2cos2 x
x
C.f(x)=2cos2 x
x
D.f(x)=2cos x
x -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是( )
A.57.2,3.6
B.57.2,56.4
C.62.8,63.6
D.62.8,3.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
 )(x∈R)的部分图象如图所示.
)(x∈R)的部分图象如图所示.
(Ⅰ)求函数f(x)的解析式并求函数f(x)的单调递增区间;
(Ⅱ)求函数f(x)的最小值并指出函数f(x)取最小值时相应的x的值.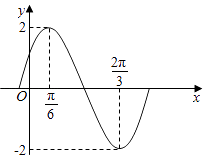
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin2
 +
+  sinωx﹣
sinωx﹣  (ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
(ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
A.(0, ]
]
B.(0, ]∪[
]∪[  ,1)
,1)
C.(0, ]
]
D.(0, ]∪[
]∪[  ,
,  ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中,  .
.(1)若
 是
是 的中点,求证:
的中点,求证:  平面
平面 ;
;(2)若
 ,求证:平面
,求证:平面 平面
平面 .
.
相关试题

