【题目】已知函数![]() (
(![]() ).
).
(1)讨论函数![]() 极值点的个数,并说明理由;
极值点的个数,并说明理由;
(2)若![]() ,
, ![]() 恒成立,求
恒成立,求![]() 的最大整数值.
的最大整数值.
参考答案:
【答案】(1)当![]() 时,
时, ![]() 在
在![]() 上没有极值点;当
上没有极值点;当![]() 时,
时, ![]() 在
在![]() 上有一个极值点.
上有一个极值点.
(2)3.
【解析】试题分析:
(1)首先对函数求导,然后分类讨论可得当![]() 时,
时, ![]() 在
在![]() 上没有极值点;当
上没有极值点;当![]() 时,
时, ![]() 在
在![]() 上有一个极值点.
上有一个极值点.
(2)结合题中所给的条件构造新函数![]() (
(![]() ),结合函数的性质可得实数
),结合函数的性质可得实数![]() 的最大整数值为3.
的最大整数值为3.
试题解析:
(1)![]() 的定义域为
的定义域为![]() ,且
,且![]() .
.
当![]() 时,
时, ![]() 在
在![]() 上恒成立,函数
上恒成立,函数![]() 在
在![]() 上单调递减.
上单调递减.
∴![]() 在
在![]() 上没有极值点;
上没有极值点;
当![]() 时,令
时,令![]() 得
得![]() ;
;
列表
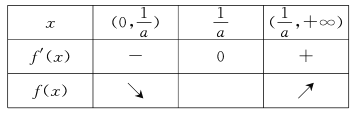
所以当![]() 时,
时, ![]() 取得极小值.
取得极小值.
综上,当![]() 时,
时, ![]() 在
在![]() 上没有极值点;
上没有极值点;
当![]() 时,
时, ![]() 在
在![]() 上有一个极值点.
上有一个极值点.
(2)对![]() ,
, ![]() 恒成立等价于
恒成立等价于![]() 对
对![]() 恒成立,
恒成立,
设函数![]() (
(![]() ),则
),则![]() (
(![]() ),
),
令函数![]() ,则
,则![]() (
(![]() ),
),
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上是增函数,
上是增函数,
又![]() ,
, ![]() ,
,
所以存在![]() ,使得
,使得![]() ,即
,即![]() ,
,
且当![]() 时,
时, ![]() ,即
,即![]() ,故
,故![]() 在
在![]() 在上单调递减;
在上单调递减;
当![]() 时,
时, ![]() ,即
,即![]() ,故
,故![]() 在
在![]() 上单调递增;
上单调递增;
所以当![]() 时,
时, ![]() 有最小值
有最小值![]() ,
,
由![]() 得
得![]() ,即
,即![]() ,
,
所以![]() ,
,
所以![]() ,又
,又![]() ,所以实数
,所以实数![]() 的最大整数值为3.
的最大整数值为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
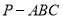 中,
中, 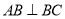 ,
, 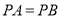 ,
, 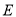 为
为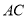 的中点.
的中点.(1)求证:
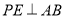 ;
;(2)设平面
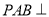 平面
平面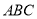 ,
, 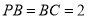 ,
, 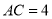 ,求二面角
,求二面角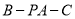 的平面角的正弦值.
的平面角的正弦值.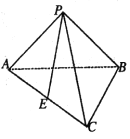
-
科目: 来源: 题型:
查看答案和解析>>【题目】某教师有相同的语文参考书3本,相同的数学参考书4本,从中取出4本赠送给4位学生,每位学生1本,则不同的赠送方法共有( )
A. 15种 B. 20种 C. 48种 D. 60种
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数
 .
.(1)若
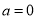 ,求不等式
,求不等式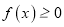 的解集;
的解集;(2)若方程
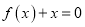 有三个不同的解,求实数
有三个不同的解,求实数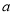 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某校歌咏比赛中,甲班、乙班、丙班、丁班均可从
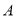 、
、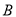 、
、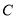 、
、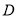 四首不同曲目中任选一首.
四首不同曲目中任选一首.(1)求甲、乙两班选择不同曲目的概率;
(2)设这四个班级总共选取了
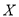 首曲目,求
首曲目,求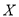 的分布列及数学期望
的分布列及数学期望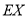 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在探究实系数一元二次方程的根与系数的关系时,可按下述方法进行:
设实系数一元二次方程
 ……①
……①在复数集
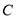 内的根为
内的根为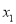 ,
,  ,则方程①可变形为
,则方程①可变形为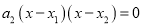 ,
,展开得
 .……②
.……②比较①②可以得到:

类比上述方法,设实系数一元
 次方程
次方程 (
( 且
且 )在复数集
)在复数集 内的根为
内的根为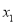 ,
, 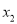 ,…,
,…,  ,则这
,则这 个根的积
个根的积 __________.
__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 (
( ,
,  )展开式的前三项的二项式系数之和为16,所有项的系数之和为1.
)展开式的前三项的二项式系数之和为16,所有项的系数之和为1.(1)求
 和
和 的值;
的值;(2)展开式中是否存在常数项?若有,求出常数项;若没有,请说明理由;
(3)求展开式中二项式系数最大的项.
相关试题

