【题目】某商品最近30天的价格f(t)(元)与时间t满足关系式:f(t)= 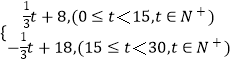 ,且知销售量g(t)与时间t满足关系式 g(t)=﹣t+30,(0≤t≤30,t∈N+),求该商品的日销售额的最大值.
,且知销售量g(t)与时间t满足关系式 g(t)=﹣t+30,(0≤t≤30,t∈N+),求该商品的日销售额的最大值.
参考答案:
【答案】解:设W(t)表示商品的日销售额(单位:元)与时间t的函数关系,
则有:W(t)=f(t)g(t)
= 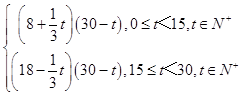 =
= 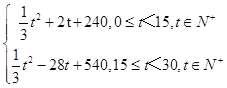
= 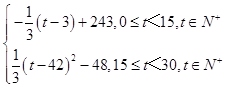 ,
,
当0≤t<15,t∈N+时,易得t=3时,W(t)取最大,且为W(3)=243;
当15≤t≤30,t∈N+时,[15,30]为减函数,则t=15时,W(t)取最大,且为W(15)=195.
所以当t=3时,该商品的日销售额最大,且为243
【解析】设W(t)表示商品的日销售额(单位:元)与时间t的函数关系,则有:W(t)=f(t)g(t),对每段化简和配方,根据二次函数的性质,分别求解每段函数的最大值,由此能求出商品的日销售额W(t)的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,椭圆C:
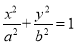 (a>b>0)的离心率为
(a>b>0)的离心率为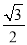 ,其左焦点到点
,其左焦点到点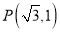 的距离为
的距离为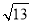 .不过原点O的直线
.不过原点O的直线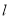 与C相交于A,B两点,且线段AB被直线OP平分.
与C相交于A,B两点,且线段AB被直线OP平分.(1)求椭圆C的方程;
(2)求
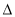 ABP的面积取最大时直线l的方程.
ABP的面积取最大时直线l的方程.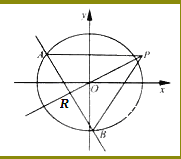
-
科目: 来源: 题型:
查看答案和解析>>【题目】设A={﹣4,2a﹣1,a2},B={a﹣5,1﹣a,9},已知A∩B={9},求a的值,并求出A∪B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(x+1),g(x)=loga(1﹣x)(a>0且a≠1).
(1)求f(x)+g(x)的定义域;
(2)判断函数f(x)+g(x)的奇偶性,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f′(x)是函数y=f(x)的导数,f′′(x)是f′(x)的导数,若方程f′′(x)有实数解x0 , 则称点(x0 , f(x0))为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数f(x)=
 x3﹣
x3﹣  x2+3x﹣
x2+3x﹣  ,请你根据这一发现,计算f(
,请你根据这一发现,计算f(  )+f(
)+f(  )+f(
)+f(  )+…+f(
)+…+f(  )= .
)= . -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位组织职工去某地参观学习,需包车前往,甲车队说:“如果领队买一张全票,其余人可享受7折优惠。”乙车队说:“你们属于团体票,按原价的7.5折优惠。”这两个车队的原价、车型都是一样的,试根据单位去的人数比较两车队的收费哪家更优惠。
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)设复数z满足|z|=1,且(3+4i)z为纯虚数,求 ;
;
(2)已知(2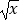 ﹣
﹣ 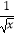 )n的展开式中所有二项式系数之和为64,求展开式的常数项.
)n的展开式中所有二项式系数之和为64,求展开式的常数项.
相关试题

