【题目】设函数f(x)=loga(1﹣![]() ),其中0<a<1.
),其中0<a<1.
(Ⅰ)证明:f(x)是(a,+∞)上的减函数;
(Ⅱ)若f(x)>1,求x的取值范围.
参考答案:
【答案】解:(Ⅰ)设0<a<x1<x2 , g(x)=1﹣![]() ,
,
则g(x1 )﹣g(x2)=(1﹣![]() )﹣(1﹣
)﹣(1﹣![]() )=
)=![]() <0,
<0,
∴g(x1 )<g(x2 ),
又∵0<a<1,
∴f(x1 )>f(x2 ),
∴f(x)在(a,+∞)递减;
(Ⅱ)∵![]() >1,
>1,
∴0<1﹣![]() <a,
<a,
∴1﹣a<![]() <1,
<1,
∵0<a<1,
∴1﹣a>0,
从而a<x<![]() ,
,
∴x的范围是(a,![]() ).
).
【解析】(Ⅰ)设0<a<x1<x2 , g(x)=1﹣![]() , 则g(x1 )﹣g(x2)=
, 则g(x1 )﹣g(x2)=![]() <0,进而f(x1 )>f(x2 ),得f(x)在(a,+∞)递减;
<0,进而f(x1 )>f(x2 ),得f(x)在(a,+∞)递减;
(Ⅱ)由![]() >1,得1﹣a<<1,从而a<x<
>1,得1﹣a<<1,从而a<x<![]() , 从而求出x的范围.
, 从而求出x的范围.
【考点精析】通过灵活运用利用导数研究函数的单调性,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减即可以解答此题.
在这个区间单调递减即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数

(1)若
 在
在 处取得极值,确定
处取得极值,确定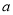 的值,并求此时曲线
的值,并求此时曲线 在点
在点 处的切线方程;
处的切线方程;(2)若
 在
在 上为减函数,求
上为减函数,求 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】数列
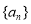 的前
的前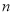 项和为
项和为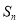 ,且
,且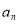 是
是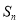 和
和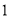 的等差中项,等差数列
的等差中项,等差数列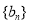 满足
满足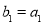 ,
,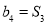 .
.(1)求数列
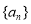 、
、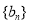 的通项公式;
的通项公式; (2)设
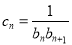 ,数列
,数列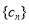 的前
的前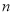 项和为
项和为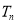 ,证明:
,证明: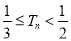 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
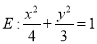 与y轴的正半轴相交于点M,且椭圆E上相异两点A、B满足直线MA,MB的斜率之积为
与y轴的正半轴相交于点M,且椭圆E上相异两点A、B满足直线MA,MB的斜率之积为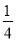 .
.(Ⅰ)证明直线AB恒过定点,并求定点的坐标;
(Ⅱ)求三角形ABM的面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=kx2+2x(k为实常数)为奇函数,函数g(x)=af(x)﹣1(a>0且a≠1).
(Ⅰ)求k的值;
(Ⅱ)求g(x)在[﹣1,2]上的最大值;
(Ⅲ)当a=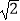 时,g(x)≤t2﹣2mt+1对所有的x∈[﹣1,1]及m∈[﹣1,1]恒成立,求实数t的取值范围.
时,g(x)≤t2﹣2mt+1对所有的x∈[﹣1,1]及m∈[﹣1,1]恒成立,求实数t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体ABCD﹣A1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有( )
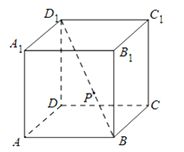
A.3个
B.4个
C.5个
D.6个 -
科目: 来源: 题型:
查看答案和解析>>【题目】有下列四个命题:
①“若
 , 则
, 则 互为相反数”的逆命题;
互为相反数”的逆命题;②“若两个三角形全等,则两个三角形的面积相等”的否命题;
③“若
 ,则
,则 有实根”的逆否命题;
有实根”的逆否命题;④“若
 不是等边三角形,则
不是等边三角形,则 的三个内角相等”逆命题;
的三个内角相等”逆命题;其中真命题为( ).
A. ①② B. ②③ C. ①③ D. ③④
相关试题

