【题目】数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() 是
是![]() 和
和![]() 的等差中项,等差数列
的等差中项,等差数列![]() 满足
满足![]() ,
,![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,证明:
,证明:![]() .
.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)证明过程详见解析.
;(2)证明过程详见解析.
【解析】
试题分析:本题主要考查等差数列与等比数列的概念、通项公式、前![]() 项和公式、数列求和等基础知识,考查运算能力、推理论证能力.第一问,先利用
项和公式、数列求和等基础知识,考查运算能力、推理论证能力.第一问,先利用![]() 是
是![]() 和
和![]() 的等差中项,得到
的等差中项,得到![]() ,由
,由![]() 求
求![]() ,注意
,注意![]() 的情况,不要漏掉,会得到
的情况,不要漏掉,会得到![]() 为等比数列,利用等比数列的通项公式,求和公式直接写出
为等比数列,利用等比数列的通项公式,求和公式直接写出![]() 和
和![]() ,再利用已知求出
,再利用已知求出![]() ,写出等差数列的通项公式;第二问,先化简
,写出等差数列的通项公式;第二问,先化简![]() 表达式,利用裂项相消法求和求
表达式,利用裂项相消法求和求![]() ,利用放缩法比较
,利用放缩法比较![]() 与
与![]() 的大小,作差法判断数列的单调性,因为数列
的大小,作差法判断数列的单调性,因为数列![]() 为递增数列,所以最小值为
为递增数列,所以最小值为![]() ,即
,即![]() ,所以
,所以![]() .
.
试题解析:(1)∵![]() 是
是![]() 和
和![]() 的等差中项,∴
的等差中项,∴![]()
当![]() 时,
时,![]() ,∴
,∴![]()
当![]() 时,
时,![]() ,
,
∴![]() ,即
,即 ![]() 3分
3分
∴数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,
为公比的等比数列,
∴![]() ,
,![]() 5分
5分
设![]() 的公差为
的公差为![]() ,
,![]() ,
,![]() ,∴
,∴![]()
∴![]() 6分
6分
(2)![]() 7分
7分
∴![]() 9分
9分
∵![]() ,∴
,∴![]() 10分
10分
![]()
∴数列![]() 是一个递增数列 ∴
是一个递增数列 ∴![]() .
.
综上所述,![]() . 12分
. 12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】经国务院批复同意,郑州成功入围国家中心城市,某校学生团针对“郑州的发展环境”对20名学生进行问卷调查打分(满分100分),得到如图1所示茎叶图.
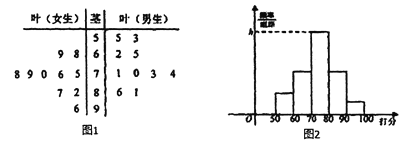
(1)分别计算男生女生打分的平均分,并用数学特征评价男女生打分的数据分布情况;
(2)如图2按照打分区间
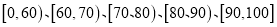 绘制的直方图中,求最高矩形的高;
绘制的直方图中,求最高矩形的高;(3)从打分在70分以下(不含70分)的同学中抽取3人,求有女生被抽中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
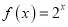 ,
, 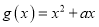 (其中
(其中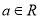 ).对于不相等的实数
).对于不相等的实数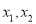 ,设
,设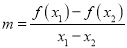 ,
, 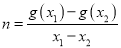 .现有如下命题:
.现有如下命题:(1)对于任意不相等的实数
 ,都有
,都有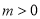 ;
;(2)对于任意的a及任意不相等的实数
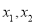 ,都有
,都有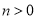 ;
;(3)对于任意的a,存在不相等的实数
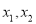 ,使得
,使得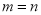 ;
;(4)对于任意的a,存在不相等的实数
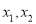 ,使得
,使得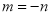 .
.其中的真命题有_____________(写出所有真命题的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数

(1)若
 在
在 处取得极值,确定
处取得极值,确定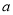 的值,并求此时曲线
的值,并求此时曲线 在点
在点 处的切线方程;
处的切线方程;(2)若
 在
在 上为减函数,求
上为减函数,求 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
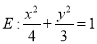 与y轴的正半轴相交于点M,且椭圆E上相异两点A、B满足直线MA,MB的斜率之积为
与y轴的正半轴相交于点M,且椭圆E上相异两点A、B满足直线MA,MB的斜率之积为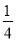 .
.(Ⅰ)证明直线AB恒过定点,并求定点的坐标;
(Ⅱ)求三角形ABM的面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=loga(1﹣
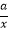 ),其中0<a<1.
),其中0<a<1.
(Ⅰ)证明:f(x)是(a,+∞)上的减函数;
(Ⅱ)若f(x)>1,求x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=kx2+2x(k为实常数)为奇函数,函数g(x)=af(x)﹣1(a>0且a≠1).
(Ⅰ)求k的值;
(Ⅱ)求g(x)在[﹣1,2]上的最大值;
(Ⅲ)当a=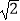 时,g(x)≤t2﹣2mt+1对所有的x∈[﹣1,1]及m∈[﹣1,1]恒成立,求实数t的取值范围.
时,g(x)≤t2﹣2mt+1对所有的x∈[﹣1,1]及m∈[﹣1,1]恒成立,求实数t的取值范围.
相关试题

