【题目】已知函数 ![]() .
.
(1)若曲线 ![]() 在点
在点 ![]() 处的切线斜率为3,且
处的切线斜率为3,且 ![]() 时
时 ![]() 有极值,求函数
有极值,求函数 ![]() 的解析式;
的解析式;
(2)在(1)的条件下,求函数 ![]() 在
在 ![]() 上的最大值和最小值.
上的最大值和最小值.
参考答案:
【答案】
(1)解:由f(1)=3, f( ![]() )=0 得a=2,b=-4 ,则函数的解析式为
)=0 得a=2,b=-4 ,则函数的解析式为 ![]()
(2)解:由f(x)=x3+2x2-4x+5 得f(x)=(x+2)(3x-2) f(x)=0得 x1=-2 ,x2= ![]()
变化情况如表:
x | -4 | (-4,-2) | -2 | (-2, |
| ( | 1 |
f(x) | + | 0 | - | 0 | + | ||
f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 | ||
函数值 | -11 | 13 |
| 4 |
所以f(x)在[-4,1]上的最大值13,最小值-11
【解析】(1)先求出原函数的导函数利用曲线f(x) 在点(1,f(1))处的切线斜率为3,且x=![]() 时,y=f(x) 有极值,联立两个方程即可求出函数f(x) 的解析。(2)确定函数的极值点,利用函数的最值在极值点处及端点处取得,即可得到结论。
时,y=f(x) 有极值,联立两个方程即可求出函数f(x) 的解析。(2)确定函数的极值点,利用函数的最值在极值点处及端点处取得,即可得到结论。
【考点精析】通过灵活运用函数的最大(小)值与导数,掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.
比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学用“五点法”画函数
 在某一个周期内的图像时,列表并填入了部分数据,如下表:
在某一个周期内的图像时,列表并填入了部分数据,如下表:
0











0
5
0
-5
0
(1)求出实数
 ;
;(2)求出函数
 的解析式;
的解析式;(3)将
 图像上所有点向左平移
图像上所有点向左平移 个单位长度,得到
个单位长度,得到 图像,求
图像,求 的图像离原点
的图像离原点 最近的对称中心.
最近的对称中心. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
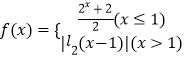 ,则函数
,则函数 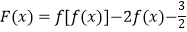 的零点个数是( )
的零点个数是( )
A.4
B.5
C.6
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为8
 ,圆环的圆心
,圆环的圆心 距离地面的高度为10
距离地面的高度为10 ,蚂蚁每12分钟爬行一圈,若蚂蚁的起始位置在最低点
,蚂蚁每12分钟爬行一圈,若蚂蚁的起始位置在最低点 处.
处.(1)试确定在时刻
 (
(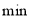 )时蚂蚁距离地面的高度
)时蚂蚁距离地面的高度 ;
;(2)在蚂蚁绕圆环爬行的一圈内,有多长时间蚂蚁距离地面超过14
 ?
?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)解不等式
 ;
;(2)若函数
 在区间
在区间 上存在零点,求实数
上存在零点,求实数 的取值范围;
的取值范围;(3)若函数
 ,其中
,其中 为奇函数,
为奇函数,  为偶函数,若不等式
为偶函数,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的函数
上的函数 是奇函数.
是奇函数.(1)求
 的值;
的值;(2)判断
 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;(3)若对任意的
 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂商为了解用户对其产品是否满意,在使用产品的用户中随机调查了80人,结果如下表:

(1)根据上述,现用分层抽样的方法抽取对产品满意的用户5人,在这5人中任选2人,求被选中的恰好是男、女用户各1人的概率;
(2)有多大把握认为用户对该产品是否满意与用户性别有关?请说明理由.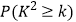
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
注:
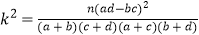
相关试题

