【题目】已知函数![]() .
.
(1)解不等式![]() ;
;
(2)若函数![]() 在区间
在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,其中
,其中![]() 为奇函数,
为奇函数, ![]() 为偶函数,若不等式
为偶函数,若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)(1,3)(2)![]() (3)
(3)![]()
【解析】试题分析:
(1)利用换元法并通过解二次不等式可得2<2x<8,可得1<x<3,即为所求.(2)分离参数可得![]() 在
在![]() 有解,设
有解,设![]() ,求出函数
,求出函数![]() 在区间
在区间![]() 上的值域即为所求范围.(3)根据题意求得
上的值域即为所求范围.(3)根据题意求得![]() 的解析式,然后通过分离参数
的解析式,然后通过分离参数![]() ,将恒成立问题转化为具体函数的最值问题,求解即可.
,将恒成立问题转化为具体函数的最值问题,求解即可.
试题解析:
(1)原不等式即为![]() ,
,
设t=2x,则不等式化为t﹣t2>16﹣9t,
即t2﹣10t+16<0,解得2<t<8,
即2<2x<8,
∴1<x<3
∴原不等式的解集为(1,3).
(2)函数![]() 在
在![]() 上有零点,
上有零点,
所以![]() 在
在![]() 上有解,
上有解,
即![]() 在
在![]() 有解.
有解.
设![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
∴![]() .
.
∵![]() 在
在![]() 有解
有解
∴![]()
故实数m的取值范围为![]() .
.
(3)由题意得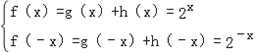 ,
,
解得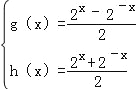 .
.
由题意得![]() ,即
,即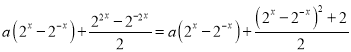
![]() 对任意
对任意![]() 恒成立,
恒成立,
令![]() ,则
,则![]() .
.
则得![]() 对任意的
对任意的![]() 恒成立,
恒成立,
∴![]() 对任意的
对任意的![]() 恒成立,
恒成立,
因为![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() .
.
所以![]() .
.
∴实数![]() 的取值范围
的取值范围![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
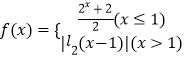 ,则函数
,则函数 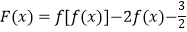 的零点个数是( )
的零点个数是( )
A.4
B.5
C.6
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为8
 ,圆环的圆心
,圆环的圆心 距离地面的高度为10
距离地面的高度为10 ,蚂蚁每12分钟爬行一圈,若蚂蚁的起始位置在最低点
,蚂蚁每12分钟爬行一圈,若蚂蚁的起始位置在最低点 处.
处.(1)试确定在时刻
 (
(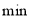 )时蚂蚁距离地面的高度
)时蚂蚁距离地面的高度 ;
;(2)在蚂蚁绕圆环爬行的一圈内,有多长时间蚂蚁距离地面超过14
 ?
?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
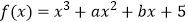 .
.
(1)若曲线 在点
在点 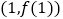 处的切线斜率为3,且
处的切线斜率为3,且 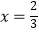 时
时 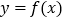 有极值,求函数
有极值,求函数  的解析式;
的解析式;
(2)在(1)的条件下,求函数 在
在 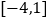 上的最大值和最小值.
上的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的函数
上的函数 是奇函数.
是奇函数.(1)求
 的值;
的值;(2)判断
 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;(3)若对任意的
 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂商为了解用户对其产品是否满意,在使用产品的用户中随机调查了80人,结果如下表:

(1)根据上述,现用分层抽样的方法抽取对产品满意的用户5人,在这5人中任选2人,求被选中的恰好是男、女用户各1人的概率;
(2)有多大把握认为用户对该产品是否满意与用户性别有关?请说明理由.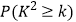
0.15
0.10
0.05
0.025
0.010
0.005
0.001
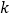
2.072
2.706
3.841
5.024
6.635
7.879
10.828
注:
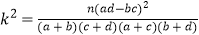
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
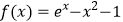 ,
, 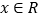
(1)求函数的图象在点 处的切线方程;
处的切线方程;
(2)当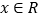 时,求证:
时,求证:  ;
;
(3)若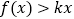 对任意的
对任意的 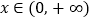 恒成立,求实数
恒成立,求实数 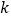 的取值范围.
的取值范围.
相关试题

