【题目】某同学用“五点法”画函数![]() 在某一个周期内的图像时,列表并填入了部分数据,如下表:
在某一个周期内的图像时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
|
|
|
|
| 0 | 5 | 0 | -5 | 0 |
(1)求出实数![]() ;
;
(2)求出函数![]() 的解析式;
的解析式;
(3)将![]() 图像上所有点向左平移
图像上所有点向左平移![]() 个单位长度,得到
个单位长度,得到![]() 图像,求
图像,求![]() 的图像离原点
的图像离原点![]() 最近的对称中心.
最近的对称中心.
参考答案:
【答案】(1)![]() (2)
(2) ![]() (3)
(3)![]()
【解析】试题分析:
(1)由表中的数据可求得函数![]() 的周期,根据“五点法”中每相邻的两点之间相差
的周期,根据“五点法”中每相邻的两点之间相差![]() 个周期可求得
个周期可求得![]() .(2)由表中数据求出
.(2)由表中数据求出![]() 后可得解析式.(3)求得函数
后可得解析式.(3)求得函数![]() 的解析式后可求得函数
的解析式后可求得函数![]() 图象的对称中心,根据题意求解即可.
图象的对称中心,根据题意求解即可.
试题解析:
(1)由题意得![]() ,
,
∴![]() .
.
∴![]() ,
,
故![]() .
.
(2)根据表中已知数据, ![]() ,所以
,所以![]() .
.
∴![]() .
.
又当![]() 时,
时, ![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() .
.
∴函数表达式![]() .
.
(3)由题意知![]()
![]()
令![]()
得![]()
所以函数![]() 图象的对称中心为
图象的对称中心为![]()
故离原点![]() 最近的对称中心为
最近的对称中心为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xlnx﹣
 x2﹣x+a,a∈R
x2﹣x+a,a∈R
(1)当a=0时,求函数f(x)的极值;
(2)若函数f(x)在其定义域内有两个不同的极值点(极值点是指函数取极值时对应的自变量的值),记为x1 , x2 , 且x1<x2 . (ⅰ)求a的取值范围;
(ⅱ)若不等式e1+λ<x1x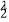 恒成立,求正实数λ的取值范围.
恒成立,求正实数λ的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的一个上界.已知函数
的一个上界.已知函数 ,
,  .
.(1)若函数
 为奇函数,求实数
为奇函数,求实数 的值;
的值;(2)在(1)的条件下,求函数
 在区间
在区间 上的所有上界构成的集合;
上的所有上界构成的集合;(3)若函数
 在
在 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
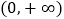 上的单调递减函数
上的单调递减函数 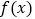 ,若
,若 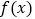 的导函数存在且满足
的导函数存在且满足 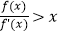 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A.
B.
C.
D.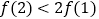
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
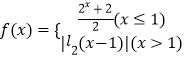 ,则函数
,则函数 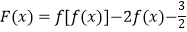 的零点个数是( )
的零点个数是( )
A.4
B.5
C.6
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为8
 ,圆环的圆心
,圆环的圆心 距离地面的高度为10
距离地面的高度为10 ,蚂蚁每12分钟爬行一圈,若蚂蚁的起始位置在最低点
,蚂蚁每12分钟爬行一圈,若蚂蚁的起始位置在最低点 处.
处.(1)试确定在时刻
 (
(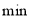 )时蚂蚁距离地面的高度
)时蚂蚁距离地面的高度 ;
;(2)在蚂蚁绕圆环爬行的一圈内,有多长时间蚂蚁距离地面超过14
 ?
?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
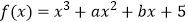 .
.
(1)若曲线 在点
在点 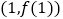 处的切线斜率为3,且
处的切线斜率为3,且 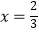 时
时 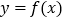 有极值,求函数
有极值,求函数  的解析式;
的解析式;
(2)在(1)的条件下,求函数 在
在 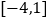 上的最大值和最小值.
上的最大值和最小值.
相关试题

