【题目】某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
(Ⅰ)设甲、乙两个班所抽取的10名同学成绩方差分别为![]() 、
、![]() ,比较
,比较![]() 、
、![]() 的大小(直接写出结果,不写过程);
的大小(直接写出结果,不写过程);
(Ⅱ)从甲班10人任取2人,设这2人中及格的人数为X,求X的分布列和期望;
(Ⅲ)从两班这20名同学中各抽取一人,在已知有人及格的条件下,求抽到乙班同学不及格的概率.

参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)观察茎叶图可得结果;(2)确定X取值为0,1,2,求出相应的概率值,得到分布列,求期望即可;(3)由茎叶图可得,甲班有4人及格,乙班有5人及格,利用条件概率公式求值.
试题解析:
(Ⅰ)由茎叶图可得![]() .
.
(Ⅱ)由题可知X取值为0,1,2.![]() ,
,![]() ,
,![]() ,
,
所以X的分布列为:
X | 0 | 1 | 2 |
P(X) |
|
|
|
所以![]() .
.
(Ⅲ)由茎叶图可得,甲班有4人及格,乙班有5人及格.设事件A=“从两班这20名同学中各抽取一人,已知有人及格”,事件B=“从两班这20名同学中各抽取一人,乙班同学不及格”.
则 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设全集U=R,集合A={x|-1≤x<3},B={x|2x-4≥x-2}.
(1)求U(A∩B);
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 为奇函数.
为奇函数.(1)求b的值;
(2)证明:函数f(x)在区间(1,+∞)上是减函数;
(3)解关于x的不等式f(1+x2)+f(-x2+2x-4)>0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择;
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率为
 .第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
.第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.方案乙:员工连续三次抽奖,每次中奖率均为
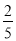 ,每次中奖均可获奖金400元.
,每次中奖均可获奖金400元.(1)求某员工选择方案甲进行抽奖所获奖金
 (元)的分布列;
(元)的分布列;(2)某员工选择方案乙与选择方案甲进行抽奖,试比较哪个方案更划算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,均值与方差都不变;
②设有一个回归方程
 ,变量x增加一个单位时,y平均增加3个单位;
,变量x增加一个单位时,y平均增加3个单位;③线性回归方程
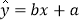 必经过点
必经过点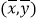 ;
;④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说现有100人吸烟,那么其中有99人患肺病.其中错误的个数是( )
A. 0
B. 1
C. 2
D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】设全集U=R,集合A={x|-1≤x<3},B={x|2x-4≥x-2}.
(1)求U(A∩B);
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是R上的奇函数,当x>0时,解析式为f(x)=
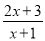 .
. (1)求f(x)在R上的解析式;
(2)用定义证明f(x)在(0,+∞)上为减函数.
相关试题

