【题目】(1)设直线l过点(2,3)且与直线2x+y+1=0垂直,l与x轴,y轴分别交于A、B两点,求|AB|;
(2)求过点A(4,-1)且在x轴和y轴上的截距相等的直线l的方程.
参考答案:
【答案】(1)2![]() ; (2)x+4y=0或x+y-3=0
; (2)x+4y=0或x+y-3=0
【解析】
(1)由题意知直线l的斜率为![]() ,设l的方程为x-2y+c=0,代入(2,3)可得c=4,即可求出A,B的坐标即可求出|AB|;
,设l的方程为x-2y+c=0,代入(2,3)可得c=4,即可求出A,B的坐标即可求出|AB|;
(2)分类讨论:直线过原点时和直线不过原点,分别求出即可。
(1)由题意知直线l的斜率为![]() ,设l的方程为x-2y+c=0,代入(2,3)可得c=4,
,设l的方程为x-2y+c=0,代入(2,3)可得c=4,
则x-2y+4=0,
令x=0,得y=2,令y=0,得x=-4,
∴A(-4,0),B(0,2),
则|AB|=![]() =2
=2![]() ;
;
(2)当直线不过原点时,设直线l的方程为x+y=c,代入(4,-1)可得c=3,此时方程为x+y-3=0,
当直线过原点时,此时方程为x+4y=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=
 ,连接CE并延长交AD于F
,连接CE并延长交AD于F 
(1)求证:AD⊥平面CFG;
(2)求平面BCP与平面DCP的夹角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C1的方程为x2+(y+1)2=4,圆C2的圆心坐标为(2,1).
(1)若圆C1与圆C2相交于A,B两点,且|AB|=
 ,求点C1到直线AB的距离;
,求点C1到直线AB的距离;(2)若圆C1与圆C2相内切,求圆C2的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,点E是AB的中点.

(1)求证:OE∥平面BCC1B1.
(2)若AC1⊥A1B,求证:AC1⊥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的三角形ABC中,一机器人从三角形ABC上的每一个顶点移动到另一个顶点,(规定:每次只能从一个顶点移动到另一个顶点),而且按逆时针方向移动的概率为顺时针方向移动的概率的3倍,假设现在机器人的初始位置为顶点A处,则通过三次移动后返回到A处的概率为________________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线
 的参数方程为
的参数方程为 (其中
(其中 为参数).现以坐标原点为极点,
为参数).现以坐标原点为极点,  轴的非负半轴为极轴建立极坐标标系,曲线
轴的非负半轴为极轴建立极坐标标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出直线
 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;(2)求直线
的直角坐标方程;(2)求直线 被曲线
被曲线 截得的线段的长度.
截得的线段的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组共有12位同学,下图是他们某次数学竞赛成绩(满分100分)的茎叶图,

其中有一个数字模糊不清,图中用
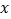 表示,规定成绩不低于80分为优秀.
表示,规定成绩不低于80分为优秀.(1)已知该12位同学竞赛成绩的中位数为78,求图中
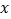 的值;
的值;(2)从该12位同学中随机选3位同学,进行竞赛试卷分析,
设其中成绩优秀的人数为
 ,求
,求 的分布列及数学期望与方差.
的分布列及数学期望与方差.
相关试题

