【题目】如图所示的三角形ABC中,一机器人从三角形ABC上的每一个顶点移动到另一个顶点,(规定:每次只能从一个顶点移动到另一个顶点),而且按逆时针方向移动的概率为顺时针方向移动的概率的3倍,假设现在机器人的初始位置为顶点A处,则通过三次移动后返回到A处的概率为________________________
参考答案:
【答案】![]() .
.
【解析】分析:先求出顺时针方向移动与逆时针方向移动的概率,分两种情况讨论,分别利用独立事件概率的乘法公式求解,然后利用互斥事件概率的加法公式求解即可.
详解:设顺时针方向移动的概率为![]() ,
,
则逆时针方向移动的概率为![]() ,
,
所以![]() ,
,
所以顺时针方向移动的概率为![]() ,
,
则逆时针方向移动的概率为![]() ,
,
初始位置为顶点![]() 处,则通过三次移动后返回到
处,则通过三次移动后返回到![]() 处,
处,
共有两种情况:三次都逆时针的概率为![]() ,
,
三次都顺时针方向移动的概率为![]() ,
,
所以通过三次移动后返回到![]() 处的概率为
处的概率为![]()
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C1的方程为x2+(y+1)2=4,圆C2的圆心坐标为(2,1).
(1)若圆C1与圆C2相交于A,B两点,且|AB|=
 ,求点C1到直线AB的距离;
,求点C1到直线AB的距离;(2)若圆C1与圆C2相内切,求圆C2的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,点E是AB的中点.

(1)求证:OE∥平面BCC1B1.
(2)若AC1⊥A1B,求证:AC1⊥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)设直线l过点(2,3)且与直线2x+y+1=0垂直,l与x轴,y轴分别交于A、B两点,求|AB|;
(2)求过点A(4,-1)且在x轴和y轴上的截距相等的直线l的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线
 的参数方程为
的参数方程为 (其中
(其中 为参数).现以坐标原点为极点,
为参数).现以坐标原点为极点,  轴的非负半轴为极轴建立极坐标标系,曲线
轴的非负半轴为极轴建立极坐标标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出直线
 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;(2)求直线
的直角坐标方程;(2)求直线 被曲线
被曲线 截得的线段的长度.
截得的线段的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组共有12位同学,下图是他们某次数学竞赛成绩(满分100分)的茎叶图,

其中有一个数字模糊不清,图中用
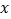 表示,规定成绩不低于80分为优秀.
表示,规定成绩不低于80分为优秀.(1)已知该12位同学竞赛成绩的中位数为78,求图中
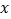 的值;
的值;(2)从该12位同学中随机选3位同学,进行竞赛试卷分析,
设其中成绩优秀的人数为
 ,求
,求 的分布列及数学期望与方差.
的分布列及数学期望与方差. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=a+bx与
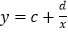 ,若对于任意一点
,若对于任意一点 ,过点
,过点 作与X轴垂直的直线,交函数y=a+bx的图象于点
作与X轴垂直的直线,交函数y=a+bx的图象于点 ,交函数
,交函数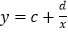 的图象于点
的图象于点 ,定义:
,定义: ,若
,若 则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数
则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数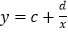 来拟合Y与X之间的关系
来拟合Y与X之间的关系(1)给定一组变量P1(1,4),P2(2,5),p3(3,6),p4(4,5.5),p5(5,5.6),p6(6,5.8),对于函数
 与函数
与函数 ,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;(2)若一组变量的散点图符合
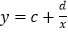 图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当
图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当 时,
时, 的值为多少.
的值为多少.
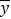











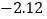
表中的

(附:对于一组数据
 ,其回归直线方程
,其回归直线方程 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为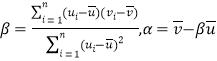 )
)
相关试题

