【题目】(1)关于![]() 的不等式
的不等式![]() 的解集不是空集,求
的解集不是空集,求![]() 的取值范围;
的取值范围;
(2)设![]() ,
,![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)利用绝对值不等式可得,![]() ,依题意即可求得
,依题意即可求得![]() 的取值范围;(2)利用柯西不等式
的取值范围;(2)利用柯西不等式![]()
![]() ,可求得
,可求得![]() ,从而可得答案.
,从而可得答案.
试题解析:(1)∵|x-3|+|x-4|≥|(x-3)-(x-4)|=1,————2分
且|x-3|+|x-4|<a的解集不是空集,∴a>1,即a的取值范围是(1,+∞).
(2)由柯西不等式,得[42+(![]() )2+22]·[(
)2+22]·[(![]() )2+(
)2+(![]() )2+(
)2+(![]() )2]
)2]
≥(4×![]() +
+![]() ×
×![]() +2×
+2×![]() )2=(x+y+z)2,
)2=(x+y+z)2,
即25×1≥(x+y+z)2.∴5≥|x+y+z|,∴-5≤x+y+z≤5.
∴x+y+z的取值范围是[-5,5].
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:sin230°+sin290°+sin2150°=
 ;
;
sin25°+sin265°+sin2125°= ;
;
sin212°+sin272°+sin2132°= ;
;
通过观察上述两等式的规律,请你写出一般性的命题,并给予的证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某公司的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如图所示.食堂某天购进了 90个面包,以
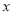 (个)(其中
(个)(其中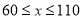 )表示面包的需求量,
)表示面包的需求量, 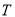 (元)表示利润.
(元)表示利润.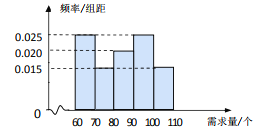
(1)根据直方图计算需求量的中位数;
(2)估计利润
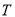 不少于100元的概率;
不少于100元的概率;(3)在直方图的需求量分组中,以需求量落入该区间的频率作为需求量在该区间的概率,求
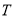 的数学期望.
的数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin(
 ﹣x)sinx﹣
﹣x)sinx﹣ 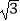 cos2x. (I)求f(x)的最小正周期和最大值;
cos2x. (I)求f(x)的最小正周期和最大值;
(II)讨论f(x)在[ ,
, 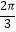 ]上的单调性.
]上的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三某班的一次测试成绩的频率分布表以及频率分布直方图中的部分数据如下,请根据此解答如下问题:
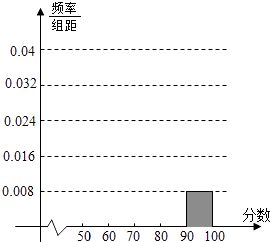
(1)求班级的总人数;
(2)将频率分布表及频率分布直方图的空余位置补充完整;
(3)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100)之间的概率.分组
频数
频率
[50,60)
0.08
[60,70)
7
[70,80)
10
[80,90)
[90,100)
2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
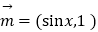 ,
,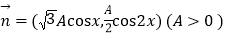 ,函数
,函数 的最大值为
的最大值为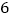 .
.
(1)求
 的大小;
的大小;(2)将函数
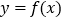 的图象向左平移
的图象向左平移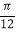 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 ,纵坐标不变,得到函数
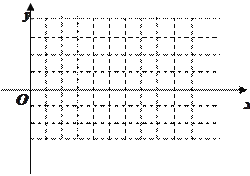
,纵坐标不变,得到函数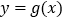 的图象,作出函数
的图象,作出函数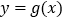 在
在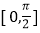 的图象.
的图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正三棱柱ABC=A1B1C1的各棱长都是4,E是BC的中点,动点F在侧棱CC1上,且不与点C重合.
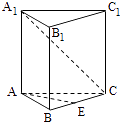
(1)当CF=1时,求证:EF⊥A1C;
(2)设二面角C﹣AF﹣E的大小为θ,求tanθ的最小值.
相关试题

