【题目】已知椭圆![]() 的对称轴为坐标轴,离心率为
的对称轴为坐标轴,离心率为![]() ,且一个焦点坐标为
,且一个焦点坐标为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,以线段
两点,以线段![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,其中点
,其中点![]() 在椭圆
在椭圆![]() 上,
上, ![]() 为坐标原点,求点
为坐标原点,求点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1)由题意可求得![]() ,
, ![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(2)首先讨论斜率存在的情况,点![]() 到直线
到直线![]() 的距离的最小值为
的距离的最小值为![]() .
.
当斜率不存在时额外讨论可得结论.
试题解析:
解:(1)由已知设椭圆![]() 的方程为
的方程为![]() ,则
,则![]() .
.
由![]() ,得
,得![]() ,
, ![]() ,
, ![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 的方程为
的方程为![]() .
.
则由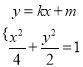 消去
消去![]() 得
得![]() .
.
![]() .①
.①
设点![]() ,
, ![]() ,
, ![]() 的坐标分别是
的坐标分别是![]() ,
, ![]() ,
, ![]() .
.
∵四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
![]() ,
,
由于点![]() 在椭圆
在椭圆![]() 上,∴
上,∴![]() ,
,
从而 ,化简得
,化简得![]() ,经检验满足①式.
,经检验满足①式.
又点![]() 到直线
到直线![]() 的距离为
的距离为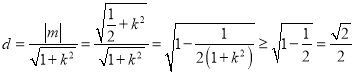 .
.
当且仅当![]() 时,等号成立.
时,等号成立.
当直线![]() 斜率不存在时,由对称性知,点
斜率不存在时,由对称性知,点![]() 一定在
一定在![]() 轴上,
轴上,
从而点![]() 的坐标为
的坐标为![]() 或
或![]() ,直线
,直线![]() 的方程为
的方程为![]() ,∴点
,∴点![]() 到直线
到直线![]() 的距离为1.
的距离为1.
∴点![]() 到直线
到直线![]() 的距离的最小值为
的距离的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是⊙O上一点,∠ACD=∠B,AD⊥CD.
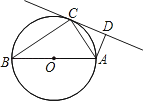
(1)求证:CD是⊙O的切线;
(2)若AD=1,OA=2,求AC的值. -
科目: 来源: 题型:
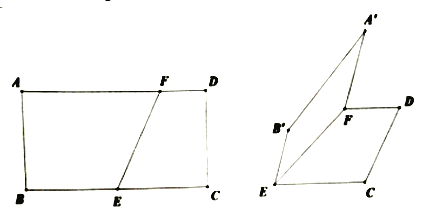
查看答案和解析>>【题目】如图,在矩形
 中,
中,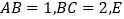 为
为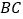 的中点,
的中点,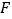 为线段
为线段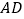 上的一点,且
上的一点,且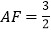 .现将四边形
.现将四边形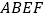 沿直线
沿直线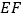 翻折,使翻折后的二面角
翻折,使翻折后的二面角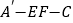 的余弦值为
的余弦值为 .
.
(1)求证:
 ;
;(2)求直线
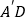 与平面
与平面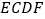 所成角的大小.
所成角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取
 名学生作为样本,得到这
名学生作为样本,得到这 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:分组
频数
频率

10
0.25

25





2
0.05
合计

1

(1)求出表中
 及图中
及图中 的值;
的值;(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间
 内的概率.
内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】图1是某公交公司1路车从起点站A站途经B站和C站,最终到达终点站D站的格点站路线图.(8×8的格点图是由边长为1的小正方形组成)
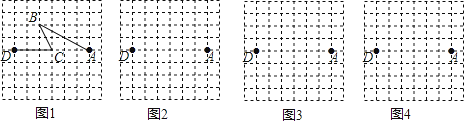
(1)求1路车从A站到D站所走的路程(精确到0.1);
(2)在图2、图3和图4的网格中各画出一种从A站到D站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复) -
科目: 来源: 题型:
查看答案和解析>>【题目】设直线
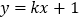 与圆
与圆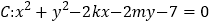 交于M、N两点,且M、N关于直线
交于M、N两点,且M、N关于直线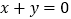 对称.
对称.(1)求m,k的值;
(2)若直线
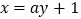 与圆C交P,Q两点,是否存在实数a使得OP⊥OQ,如果存在,求出a的值;如果不存在,请说明理由.
与圆C交P,Q两点,是否存在实数a使得OP⊥OQ,如果存在,求出a的值;如果不存在,请说明理由.
相关试题

