【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求整数
恒成立,求整数![]() 的最小值.
的最小值.
参考答案:
【答案】(1) 当![]() 时,
时, ![]() 的单调递增区间为
的单调递增区间为![]() ,无减区间,
,无减区间,
当![]() 时,
时, ![]() 的单调递增区间为
的单调递增区间为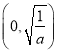 ,单调递减区间为
,单调递减区间为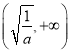 ;(2)2.
;(2)2.
【解析】试题分析:
(1)首先对函数求导,然后对参数分类讨论可得当![]() 时,
时, ![]() 的单调递增区间为
的单调递增区间为![]() ,无减区间,
,无减区间,
当![]() 时,
时, ![]() 的单调递增区间为
的单调递增区间为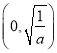 ,单调递减区间为
,单调递减区间为 ;
;
(2)将原问题转化为![]() 在
在![]() 上恒成立,考查函数
上恒成立,考查函数![]() 的性质可得整数
的性质可得整数![]() 的最小值是2.
的最小值是2.
试题解析:
(1) ![]() ,函数
,函数![]() 的定义域为
的定义域为![]() .
.
当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,令
时,令![]() ,则
,则![]() 或
或![]() (舍负),
(舍负),
当![]() 时,
时, ![]() ,
, ![]() 为增函数,
为增函数,
当![]() 时,
时, ![]() ,
, ![]() 为减函数,
为减函数,
∴当![]() 时,
时, ![]() 的单调递增区间为
的单调递增区间为![]() ,无减区间,
,无减区间,
当![]() 时,
时, ![]() 的单调递增区间为
的单调递增区间为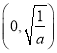 ,单调递减区间为
,单调递减区间为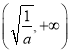 .
.
(2)解法一:由![]() 得
得![]() ,
,
∵![]() ,
,
∴原命题等价于![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,
,
则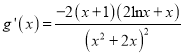 ,
,
令![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
由![]() ,
, ![]() ,
,
∴存在唯一![]() ,使
,使![]() ,
, ![]() .
.
∴当![]() 时,
时, ![]() ,
, ![]() 为增函数,
为增函数,
当![]() 时,
时, ![]() ,
, ![]() 为减函数,
为减函数,
∴![]() 时,
时, ![]() ,
,
∴![]() ,
,
又![]() ,则
,则![]() ,
,
由![]() ,所以
,所以![]() .
.
故整数![]() 的最小值为2.
的最小值为2.
解法二: ![]() 得,
得,
![]() ,
,
令![]() ,
,
![]() ,
,
①![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递减,
上单调递减,
∵![]() ,∴该情况不成立.
,∴该情况不成立.
②![]() 时,
时, ![]()
当![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
∴![]() ,
,
![]() 恒成立
恒成立![]() ,
,
即![]() .
.
令![]() ,显然
,显然![]() 为单调递减函数.
为单调递减函数.
由![]() ,且
,且![]() ,
, ![]() ,
,
∴当![]() 时,恒有
时,恒有![]() 成立,
成立,
故整数![]() 的最小值为2.
的最小值为2.
综合①②可得,整数![]() 的最小值为2.
的最小值为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
. (1)讨论函数
 在定义域内的极值点的个数;
在定义域内的极值点的个数;(2)若函数
 在
在 处取得极值,对任意的
处取得极值,对任意的 恒成立,
恒成立, ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
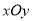 中,曲线
中,曲线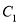 的参数方程为:
的参数方程为: 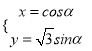 (
(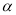 为参数),以原点
为参数),以原点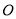 为极点,
为极点, 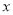 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线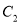 的极坐标方程为
的极坐标方程为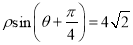 .
.(1)求直角坐标系下曲线
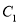 与曲线
与曲线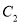 的方程;
的方程;(2)设
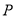 为曲线
为曲线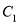 上的动点,求点
上的动点,求点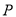 到
到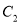 上点的距离的最大值,并求此时点
上点的距离的最大值,并求此时点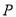 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】近几年来,我国许多地区经常出现干旱现象,为抗旱经常要进行人工降雨,现由天气预报得知,某地在未来5天的指定时间的降雨概率是:前3天均为
 ,后2天均为
,后2天均为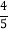 ,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.
,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.(1)求至少有1天需要人工降雨的概率;
(2)求不需要人工降雨的天数
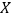 的分布列和期望.
的分布列和期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次抽样调查中测得样本的6组数据,得到一个变量
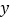 关于
关于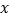 的回归方程模型,其对应的数值如下表:
的回归方程模型,其对应的数值如下表: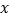
2
3
4
5
6
7
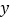
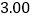
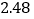
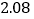
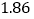
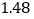
(1)请用相关系数
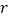 加以说明
加以说明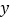 与
与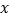 之间存在线性相关关系(当
之间存在线性相关关系(当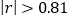 时,说明
时,说明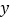 与
与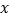 之间具有线性相关关系);
之间具有线性相关关系);(2)根据(1)的判断结果,建立
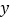 关于
关于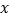 的回归方程并预测当
的回归方程并预测当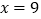 时,对应的
时,对应的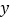 值为多少(
值为多少(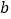 精确到
精确到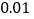 ).
).附参考公式:回归方程
 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: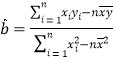 ,
,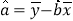 ,相关系数
,相关系数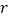 公式为:
公式为: .
.参考数据:
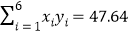 ,
,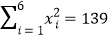 ,
,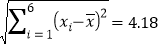 ,
,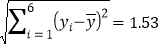 .
. -
科目: 来源: 题型:
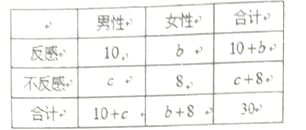
查看答案和解析>>【题目】“中国式过马路” 存在很大的交通安全隐患,某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如图的
 列联表.已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是
列联表.已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是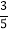 .
.(1)求
 列联表中的
列联表中的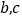 的值;
的值;
(2)根据列联表中的数据,判断是否有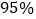 把握认为反感“中国式过马路”与性别有关?
把握认为反感“中国式过马路”与性别有关?参考公式:
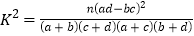 ,
,
临界值表:

-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂需要确定加工某大型零件所花费的时间,连续4天做了4次统计,得到的数据如下:
零件的个数
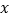 (个)
(个)2
3
4
5
加工的时间
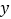 (小时)
(小时)2.5
3
4
5.5
(1)在直角坐标系中画出以上数据的散点图,求出
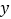 关于
关于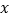 的回归方程
的回归方程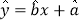 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线; 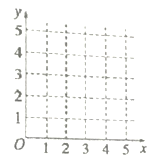
(2)试预测加工10个零件需要多少时间?
参考公式:两个具有线性关系的变量的一组数据:
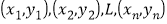 ,
,其回归方程为
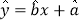 ,其中
,其中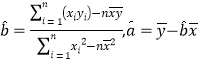
相关试题

