【题目】近几年来,我国许多地区经常出现干旱现象,为抗旱经常要进行人工降雨,现由天气预报得知,某地在未来5天的指定时间的降雨概率是:前3天均为![]() ,后2天均为
,后2天均为![]() ,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.
,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.
(1)求至少有1天需要人工降雨的概率;
(2)求不需要人工降雨的天数![]() 的分布列和期望.
的分布列和期望.
参考答案:
【答案】(1)![]() (2) x的分布列是:
(2) x的分布列是:
x | 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
3.1
【解析】(1)5天全不需要人工降雨的概率是P1=()3·()2=![]() ,故至少有1天需要人工降雨的概率是1-P1=1-
,故至少有1天需要人工降雨的概率是1-P1=1-![]() =
=![]() .
.
(2)x的取值是0,1,2,3,4,5,由(1)知5天不需要人工降雨的概率是:P(x=5)=P1=![]() ,
,
4天不需要人工降雨的概率是:
P(x=4)=()3![]() ×+
×+![]() ()3()2=
()3()2=![]()
=![]() ,
,
3天不需要人工降雨的概率是:
P(x=3)=![]() ()3()2+
()3()2+![]() ()3
()3![]() ()()+()3()2=
()()+()3()2=![]() ,
,
2天不需要人工降雨的概率是:
P(x=2)=![]() ()3()2+
()3()2+![]() ()3
()3![]() ()×()+()3×()2=
()×()+()3×()2=![]() ,
,
1天不需要人工降雨的概率是:
P(x=1)=![]() ()3()2+()3
()3()2+()3![]() ()()=
()()=![]() ,
,
0天不需要人工降雨的概率是:
P(x=0)=()3()2=![]() ,
,
故不需要人工降雨的天数x的分布列是:
x | 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
不需要人工降雨的天数x的期望是:
E(x)=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() +4×
+4×![]() +5×
+5×![]() =3.1.
=3.1.
【方法技巧】求离散型随机变量均值与方差的基本方法
(1)定义法:已知随机变量的分布列求它的均值、方差和标准差,可直接按定义(公式)求解.
(2)性质法:已知随机变量ξ的均值与方差,求ξ的线性函数η=aξ+b的均值与方差,可直接利用均值、方差的性质求解.
(3)公式法:如能分析所给随机变量是服从常用的分布(如两点分布,二项分布等),可直接利用它们的均值、方差公式求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知长方形
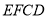 ,
, 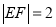 ,
, 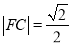 ,以
,以 的中点
的中点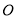 为原点,建立如图所示的平面直角坐标系
为原点,建立如图所示的平面直角坐标系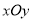 .
.(1)求以
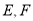 为焦点,且过
为焦点,且过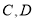 两点的椭圆的标准方程;
两点的椭圆的标准方程;(2)在(1)的条件下,过点
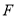 作直线
作直线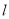 与椭圆交于不同的两点
与椭圆交于不同的两点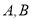 ,设
,设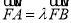 ,点
,点 坐标为
坐标为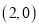 ,若
,若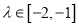 ,求
,求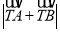 的取值范围.
的取值范围.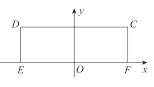
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
. (1)讨论函数
 在定义域内的极值点的个数;
在定义域内的极值点的个数;(2)若函数
 在
在 处取得极值,对任意的
处取得极值,对任意的 恒成立,
恒成立, ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
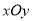 中,曲线
中,曲线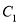 的参数方程为:
的参数方程为: 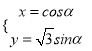 (
(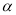 为参数),以原点
为参数),以原点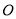 为极点,
为极点, 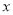 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线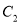 的极坐标方程为
的极坐标方程为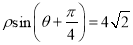 .
.(1)求直角坐标系下曲线
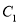 与曲线
与曲线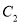 的方程;
的方程;(2)设
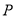 为曲线
为曲线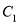 上的动点,求点
上的动点,求点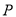 到
到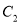 上点的距离的最大值,并求此时点
上点的距离的最大值,并求此时点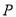 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求函数
 的单调区间;
的单调区间;(2)若关于
 的不等式
的不等式 恒成立,求整数
恒成立,求整数 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次抽样调查中测得样本的6组数据,得到一个变量
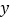 关于
关于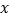 的回归方程模型,其对应的数值如下表:
的回归方程模型,其对应的数值如下表: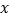
2
3
4
5
6
7
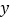
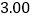
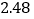
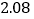
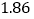
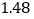
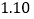
(1)请用相关系数
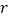 加以说明
加以说明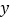 与
与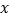 之间存在线性相关关系(当
之间存在线性相关关系(当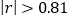 时,说明
时,说明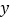 与
与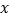 之间具有线性相关关系);
之间具有线性相关关系);(2)根据(1)的判断结果,建立
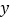 关于
关于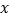 的回归方程并预测当
的回归方程并预测当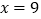 时,对应的
时,对应的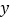 值为多少(
值为多少(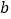 精确到
精确到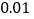 ).
).附参考公式:回归方程
 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: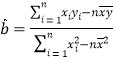 ,
,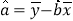 ,相关系数
,相关系数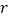 公式为:
公式为: .
.参考数据:
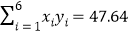 ,
,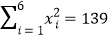 ,
,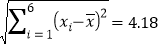 ,
,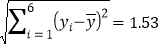 .
. -
科目: 来源: 题型:
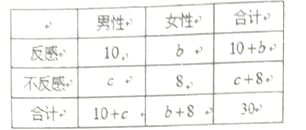
查看答案和解析>>【题目】“中国式过马路” 存在很大的交通安全隐患,某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如图的
 列联表.已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是
列联表.已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是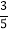 .
.(1)求
 列联表中的
列联表中的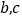 的值;
的值;
(2)根据列联表中的数据,判断是否有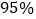 把握认为反感“中国式过马路”与性别有关?
把握认为反感“中国式过马路”与性别有关?参考公式:
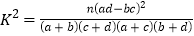 ,
,
临界值表:

相关试题

