【题目】已知椭圆C的中心在原点,一个焦点F(﹣2,0),且长轴长与短轴长的比是 ![]() .
.
(1)求椭圆C的方程;
(2)设点M(m,0)在椭圆C的长轴上,点P是椭圆上任意一点.当 ![]() 最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
参考答案:
【答案】
(1)解:设椭圆C的方程为 ![]() .
.
由题意 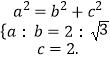
解得a2=16,b2=12.
所以椭圆C的方程为 ![]()
(2)设P(x,y)为椭圆上的动点,由于椭圆方程为 ![]() ,故﹣4≤x≤4.
,故﹣4≤x≤4.
因为 ![]() ,
,
所以 ![]() =
= ![]() .
.
因为当 ![]() 最小时,点P恰好落在椭圆的右顶点,
最小时,点P恰好落在椭圆的右顶点,
即当x=4m时, ![]() 取得最小值.而x∈[﹣4,4],
取得最小值.而x∈[﹣4,4],
故有4m≥4,解得m≥1.
又点M在椭圆的长轴上,即﹣4≤m≤4.
故实数m的取值范围是m∈[1,4].
【解析】(1)由椭圆的一个焦点F(﹣2,0)可知c=2,且长轴长与短轴长的比即![]() 可求出椭圆方程。
可求出椭圆方程。
(2)设P(x,y)为椭圆上的动点,根据椭圆的性质可以判断x的范围。代入![]() .点P恰好落在椭圆的右顶点,
.点P恰好落在椭圆的右顶点, ![]() 最小时.解得m的范围。
最小时.解得m的范围。
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
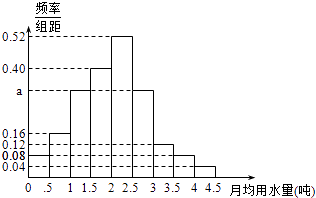
(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准x(吨),估计x的值,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆
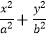 =1(a>b>0),F1 , F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
=1(a>b>0),F1 , F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.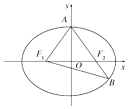
(1)若∠F1AB=90°,求椭圆的离心率;
(2)若椭圆的焦距为2,且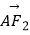 =2
=2 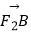 ,求椭圆的方程.
,求椭圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一学生共有500人,为了了解学生的历史学习情况,随机抽取了50名学生,对他们一年来4次考试的历史平均成绩进行统计,得到频率分布直方图如图所示,后三组频数成等比数列.
(1)求第五、六组的频数,补全频率分布直方图;
(2)若每组数据用该组区间中点值(例如区间[70,80)的中点值是
75作为代表,试估计该校高一学生历史成绩的平均分;
(3)估计该校高一学生历史成绩在70~100分范围内的人数.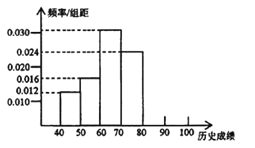
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的角
的角 所对的边份别为
所对的边份别为 ,且
,且
(1)求角
 的大小;
的大小;(2)若
 ,求
,求 的周长
的周长 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到如下列联表(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
常喝
不常喝
合计
肥胖
2
不肥胖
18
合计
30
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为
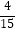 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)现从常喝碳酸饮料且肥胖的学生中(2名女生),抽取2人参加电视节目,则正好抽到一男一女的概率是多少P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
K
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:K2=
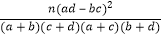 ,其中n=a+b+c+d)
,其中n=a+b+c+d) -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
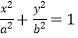 (a>b>0)与直线x+y=1交于P、Q两点,且OP⊥OQ,其中O为坐标原点.
(a>b>0)与直线x+y=1交于P、Q两点,且OP⊥OQ,其中O为坐标原点.
(1)求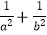 的值;
的值;
(2)若椭圆的离心率e满足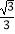 ≤e≤
≤e≤ 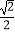 ,求椭圆长轴的取值范围.
,求椭圆长轴的取值范围.
相关试题

