【题目】椭圆 ![]() (a>b>0)与直线x+y=1交于P、Q两点,且OP⊥OQ,其中O为坐标原点.
(a>b>0)与直线x+y=1交于P、Q两点,且OP⊥OQ,其中O为坐标原点.
(1)求 ![]() 的值;
的值;
(2)若椭圆的离心率e满足 ![]() ≤e≤
≤e≤ ![]() ,求椭圆长轴的取值范围.
,求椭圆长轴的取值范围.
参考答案:
【答案】
(1)解:设P(x1,y1),Q(x2,y2)由OP⊥OQ 可得 x 1x 2+y1 y 2=0
∵y1=1﹣x1,y2=1﹣x2
∴2x1x2﹣(x1+x2)+1=0①又将y=1﹣x代入 ![]() 可得(a2+b2)x2﹣2a2x+a2(1﹣b2)=0
可得(a2+b2)x2﹣2a2x+a2(1﹣b2)=0
∵△>0∴ ![]() ,
, ![]()
代入①化简得 ![]() .
.
(2)∵ ![]()
∴ ![]()
∴ ![]()
又由(1)知 ![]()
∴ ![]() ∴
∴ ![]() ,
,
∴长轴 2a∈[ ![]() ].
].
【解析】(1)设P(x1,y1),Q(x2,y2)。由P,Q分别在椭圆上,直线上,OP⊥OQ联立方程组即可求出答案。
(2)由![]() 且
且![]() 求出a的范围。
求出a的范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的中心在原点,一个焦点F(﹣2,0),且长轴长与短轴长的比是
 .
.
(1)求椭圆C的方程;
(2)设点M(m,0)在椭圆C的长轴上,点P是椭圆上任意一点.当 最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的角
的角 所对的边份别为
所对的边份别为 ,且
,且
(1)求角
 的大小;
的大小;(2)若
 ,求
,求 的周长
的周长 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到如下列联表(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
常喝
不常喝
合计
肥胖
2
不肥胖
18
合计
30
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为
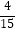 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)现从常喝碳酸饮料且肥胖的学生中(2名女生),抽取2人参加电视节目,则正好抽到一男一女的概率是多少P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
K
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:K2=
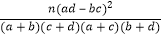 ,其中n=a+b+c+d)
,其中n=a+b+c+d) -
科目: 来源: 题型:
查看答案和解析>>【题目】十八届五中全会公报指出:努力促进人口均衡发展,坚持计划生育的基本国策,完善人口发展战略,全面实施一对夫妇可生育两个孩子的政策,提高生殖健康、妇幼保健、托幼等公共服务水平.为了解适龄公务员对放开生育二胎政策的态度,某部门随机调查了100位30到40岁的公务员,得到情况如下表:
男公务员
女公务员
生二胎
40
20
不生二胎
20
20
(1)是否有95%以上的把握认为“生二胎与性别有关”,并说明理由;
(2)把以上频率当概率,若从社会上随机抽取3位30到40岁的男公务员,记其中生二胎的人数为X,求随机变量X的分布列,数学期望.
附:K2=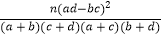
P(K2≥k0)
0.050
0.010
0.001
k0
3.841
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:其中正确命题的序号是 .
①设a,b是非零实数,若a<b,则ab2<a2b;
②若a<b<0,则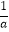 >
>  ;
;
③函数y=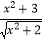 的最小值是2;
的最小值是2;
④若x,y是正数,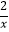 +
+ 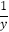 =1,则x+2y的最小值为8.
=1,则x+2y的最小值为8. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x﹣3y﹣6=0,点T(﹣1,1)在AD边所在直线上.

(1)AD边所在直线的方程;
(2)矩形ABCD外接圆的方程.
相关试题

