【题目】为了增强消防安全意识,某中学对全体学生做了一次消防知识讲座,从男生中随机抽取![]() 人,从女生中随机抽取
人,从女生中随机抽取![]() 人参加消防知识测试,统计数据得到如下列联表:
人参加消防知识测试,统计数据得到如下列联表:
优秀 | 非优秀 | 总计 | |
男生 |
|
|
|
女生 |
|
|
|
总计 |
|
|
|
(1)试判断能否有![]() 的把握认为消防知识的测试成绩优秀与否与性别有关;
的把握认为消防知识的测试成绩优秀与否与性别有关;
附:![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2)为了宣传消防知识,从该校测试成绩获得优秀的同学中采用分层抽样的方法,随机选出![]() 人组成宣传小组.现从这
人组成宣传小组.现从这![]() 人中随机抽取
人中随机抽取![]() 人到校外宣传,求到校外宣传的同学中男生人数
人到校外宣传,求到校外宣传的同学中男生人数![]() 的分布列和数学期望.
的分布列和数学期望.
参考答案:
【答案】(1) 没有![]() 的把握认为测试成绩优秀与否与性别有关(2)见解析
的把握认为测试成绩优秀与否与性别有关(2)见解析
【解析】
⑴将表中数据代入公式,对比对立性检验临界值表,即可得到结论
⑵根据古典概型的计算方法计算出![]() 可能的取值为
可能的取值为![]() 的概率,写出分布列,计算出期望即可
的概率,写出分布列,计算出期望即可
(1)因为![]() 的观测值
的观测值
![]()
![]() ,
,
所以没有![]() 的把握认为测试成绩优秀与否与性别有关.
的把握认为测试成绩优秀与否与性别有关.
(2)用分层抽样的方法抽取时抽取比例是![]() ,
,
则抽取女生![]() 人,抽取男生
人,抽取男生![]() 人.
人.
依题意,![]() 可能的取值为
可能的取值为![]() ,
,![]() ,
,![]() .
.
![]() ;
;![]() ;
;
![]() .
.
![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
![]() 的数学期望为:
的数学期望为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段
 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.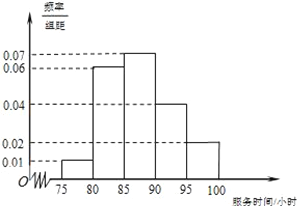
(1)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(2)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。

(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,侧面
中,侧面 底面
底面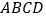 ,底面
,底面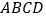 为矩形,
为矩形,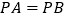 ,
,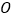 为
为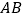 的中点,
的中点, .
.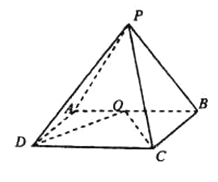
(1)求证:
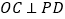 ;
;(2)若
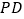 与平面
与平面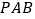 所成的角为
所成的角为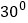 ,求二面角
,求二面角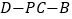 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某文体局为了解“跑团”每月跑步的平均里程,收集并整理了2018年1月至2018年11月期间“跑团”每月跑步的平均里程(单位:公里)的数据,绘制了下面的折线图.根据折线图,下列结论正确的是( )

A. 月跑步平均里程的中位数为6月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在8、9月
D. 1月至5月的月跑步平均里程相对于6月至11月,波动性更小,变化比较平稳
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动,在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示.

(1)分别计算这10名同学中,男女生测试的平均成绩;
(2)若这10名同学中,男生和女生的国学素养测试成绩的标准差分别为S1,S2,试比较S1与S2的大小(不必计算,只需直接写出结果);
(3)规定成绩大于等于75分为优良,从这10名同学中随机选取一男一女两名同学,求这两名同学的国学素养测试成绩均为优良的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)若函数
 的图像与
的图像与 轴无交点,求
轴无交点,求 的取值范围;
的取值范围;(2)若方程
 在区间
在区间 上存在实根,求
上存在实根,求 的取值范围;
的取值范围;(3)设函数
 ,
, ,当
,当 时若对任意的
时若对任意的 ,总存在
,总存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
相关试题

