【题目】如下图,三棱柱![]() 中,侧面
中,侧面![]()
![]() 底面
底面![]() ,
, ![]() ,且
,且![]() ,O为
,O为![]() 中点.
中点.
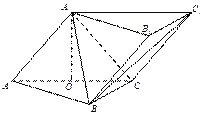
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦;
所成角的正弦;
(Ⅲ)在![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点![]() 的位置.
的位置.
参考答案:
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() 为
为![]() 的中点.
的中点.
【解析】(1)因为侧面![]() 底面
底面![]() ,所以只需证明
,所以只需证明![]() 即可.
即可.
(2)可以以O为原点,ON,OC,OA1所在直线为x,y,z轴建立空间直角坐标系,然后用向量的方法求解线面角的问题.
(3)在(2)的基础上也可以用向量来求点E位置.也可以取BC的中点M,连接OM,取BC1的中点E,连接ME,则OM//AB,ME//BB1//AA1,所以平面OMB//平面AA1B,所以OE//平面![]() .从而确定E为BC1的中点.
.从而确定E为BC1的中点.
(Ⅰ)证明:因为![]() ,且O为AC的中点,
,且O为AC的中点,
所以![]()
又由题意可知,平面![]() 平面
平面![]() ,交线为
,交线为![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
(Ⅱ)如图,以O为原点, ![]() 所在直线分别为x,y,z轴建立空间直角坐标系.
所在直线分别为x,y,z轴建立空间直角坐标系.
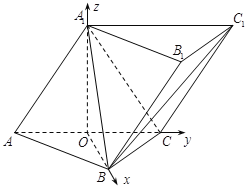
由题意可知, ![]() 又
又![]()
![]()
所以得: ![]()
则有: ![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,则有
,则有
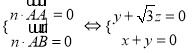 ,令
,令![]() ,得
,得![]()
所以![]()
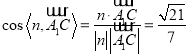
因为直线![]() 与平面
与平面![]() 所成角
所成角![]() 和向量
和向量![]() 与
与![]() 所成锐角互余,所以
所成锐角互余,所以![]()
(Ⅲ)设![]()
即![]() ,得
,得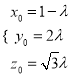
所以![]() 得
得![]()
令![]() 平面
平面![]() ,得
,得![]() ,
,
即![]() 得
得![]()
即存在这样的点E,E为![]() 的中点
的中点
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)的定义域为D,满足:①f(x)在D内是单调函数;②存在[
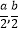 ]D,使得f(x)在[
]D,使得f(x)在[ 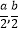 ]上的值域为[a,b],那么就称函数y=f(x)为“优美函数”,若函数f(x)=logc(cx﹣t)(c>0,c≠1)是“优美函数”,则t的取值范围为( )
]上的值域为[a,b],那么就称函数y=f(x)为“优美函数”,若函数f(x)=logc(cx﹣t)(c>0,c≠1)是“优美函数”,则t的取值范围为( )
A.(0,1)
B.(0, )
)
C.(﹣∞, )
)
D.(0, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙丙丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为
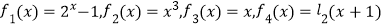 , 有以下结论:
, 有以下结论:
①当x>1时,甲在最前面;
②当x>1时,乙在最前面;
③当0<x<1时,丁在最前面,当x>1时,丁在最后面;
④丙不可能在最前面,也不可能最最后面;
⑤如果它们已知运动下去,最终在最前面的是甲.
其中,正确结论的序号为(把正确结论的序号都填上,多填或少填均不得分) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,隔河看两目标A、B,但不能到达,在岸边选取相距
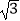 km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离.
km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离. 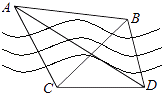
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
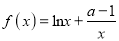 ,
, 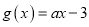 (
(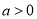 ).
).(1)求函数
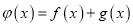 的单调增区间;
的单调增区间;(2)当
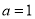 时,记
时,记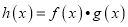 ,是否存在整数
,是否存在整数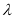 ,使得关于
,使得关于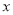 的不等式
的不等式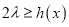 有解?若存在,请求出
有解?若存在,请求出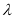 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于数列{an},定义
 为{an}的“优值”,现在已知某数列{an}的“优值”
为{an}的“优值”,现在已知某数列{an}的“优值”  ,记数列{an﹣kn}的前n项和为Sn , 若Sn≤S5对任意的n∈N+恒成立,则实数k的最大值为 .
,记数列{an﹣kn}的前n项和为Sn , 若Sn≤S5对任意的n∈N+恒成立,则实数k的最大值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面内一动点
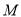 与两定点
与两定点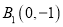 和
和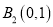 连线的斜率之积等于
连线的斜率之积等于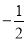 .
.(Ⅰ)求动点
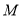 的轨迹
的轨迹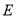 的方程;
的方程;(Ⅱ)设直线
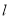 :
: 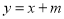 (
( )与轨迹
)与轨迹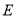 交于
交于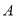 、
、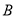 两点,线段
两点,线段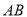 的垂直平分线交
的垂直平分线交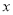 轴于点
轴于点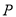 ,当
,当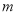 变化时,求
变化时,求 面积的最大值.
面积的最大值.
相关试题

