【题目】已知函数![]() .
.
(1)试讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个极值点
有两个极值点![]() ,
, ![]() ,且
,且![]() ,求证:
,求证: ![]() .
.
参考答案:
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)求导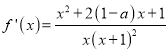 ,
, ![]() ,讨论
,讨论![]() 两种情况即可得解(2)
两种情况即可得解(2)![]() ,
, ![]() 由题意
由题意![]() ,
, ![]() 是方程
是方程![]() 的两个根,所以
的两个根,所以![]() ,①
,① ![]() ,②联立①②得出
,②联立①②得出![]() ,所以
,所以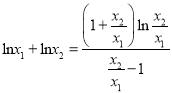 令
令![]() ,所以
,所以![]() ,
, ![]() ,因此只需证明当
,因此只需证明当![]() 时,不等式
时,不等式![]()
![]() 成立即可,即不等式
成立即可,即不等式![]() 成立,构造差函数研究单调性即可得证.
成立,构造差函数研究单调性即可得证.
试题解析:
(1)函数![]() 的定义域为
的定义域为![]() ,
, 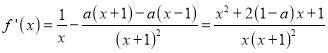 ,
,
令![]() ,
, ![]() ,
,
当![]() 时,解得
时,解得![]() ,此时
,此时![]() 在
在![]() 上恒成立,
上恒成立,
故可得![]() 在
在![]() 上恒成立,即当
上恒成立,即当![]() 时,
时, ![]() 在
在![]() 上单调递增.
上单调递增.
当![]() 时,解得
时,解得![]() 或
或![]() ,
,
方程![]() 的两根为
的两根为![]() 和
和![]() ,
,
当![]() 时,可知
时,可知![]() ,
, ![]() ,此时在
,此时在![]() 上
上![]() ,
, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,易知
时,易知![]() ,
, ![]() ,此时可得
,此时可得![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
综上可知,当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 在区间
在区间![]() 和区间
和区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
(2)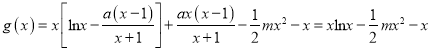 ,
,
![]() ,由题意
,由题意![]() ,
, ![]() 是方程
是方程![]() 的两个根,所以
的两个根,所以![]() ,①
,①
![]() ,②
,②
①②两式相加可得![]() ,③
,③
①②两式相减可得![]() ,④
,④
由③④两式消去![]() 可得
可得![]() ,
,
所以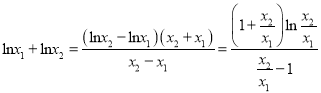 ,
,
设![]() ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
, ![]() ,
,
因此只需证明当![]() 时,不等式
时,不等式![]()
![]() 成立即可,即不等式
成立即可,即不等式![]() 成立.
成立.
设函数![]() ,由(1)可知,
,由(1)可知, ![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,即证得当
,即证得当![]() 时,
时, ![]() ,亦即证得
,亦即证得![]() ,
,
所以![]() ,即证得
,即证得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知角
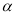 始边与
始边与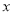 轴的非负半轴重合,与圆
轴的非负半轴重合,与圆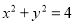 相交于点
相交于点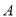 ,终边与圆
,终边与圆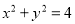 相交于点
相交于点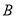 ,点
,点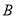 在
在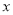 轴上的射影为
轴上的射影为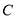 ,
, 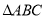 的面积为
的面积为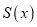 ,函数
,函数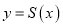 的图象大致是( )
的图象大致是( )A.
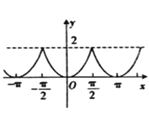 B.
B. 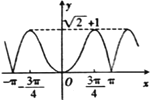
C.
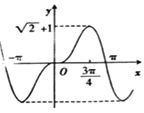 D.
D. 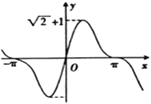
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在直角梯形
 中,
中, 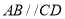 ,
, 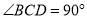 ,
, 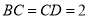 ,
, 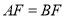 ,
, 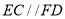 ,
, 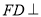 底面
底面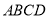 ,
, 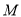 是
是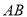 的中点.
的中点.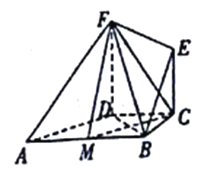
(1)求证:平面
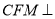 平面
平面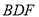 ;
;(2)若
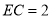 ,
, 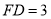 ,求平面
,求平面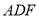 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校400名学生在一次百米赛跑测试中,成绩全部都在12秒到17秒之间,现抽取其中50个样本,将测试结果按如下方式分成五组:第一组
 ,第二组
,第二组 ,…,第五组
,…,第五组 ,如图所示的是按上述分组方法得到的频率分布直方图.
,如图所示的是按上述分组方法得到的频率分布直方图.
(1)请估计该校400名学生中,成绩属于第三组的人数;
(2)请估计样本数据的中位数(精确到0.01);
(3)若样本第一组中只有一名女生,其他都是男生,第五组则只有一名男生,其他都是女生,现从第一、第五组中各抽取2名同学组成一个特色组,设其中男同学的人数为
 ,求
,求 的分布列和期望.
的分布列和期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
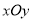 中,以
中,以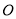 为极点,
为极点, 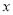 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线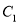 的方程是
的方程是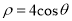 ,将
,将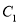 向上平移2个单位得到曲线
向上平移2个单位得到曲线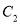 .
. (1)求曲线
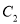 的极坐标方程;
的极坐标方程;(2)直线
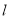 的参数方程为
的参数方程为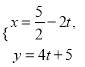 (
(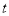 为参数),判断直线
为参数),判断直线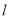 与曲线
与曲线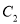 的位置关系.
的位置关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为2的圆内有两条圆弧,一质点M自点A开始沿弧A-B-C-O-A-D-C做匀速运动,则其在水平方向(向右为正)的速度
 的图像大致为( )
的图像大致为( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
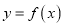 对定义域D内的每一个x1,都存在唯一的x2∈D,使得
对定义域D内的每一个x1,都存在唯一的x2∈D,使得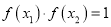 成立,则称f (x)为“自倒函数”.给出下列命题:
成立,则称f (x)为“自倒函数”.给出下列命题:①
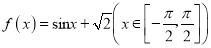 是自倒函数;
是自倒函数;②自倒函数f (x)可以是奇函数;
③自倒函数f (x)的值域可以是R;
④若
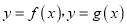 都是自倒函数,且定义域相同,则
都是自倒函数,且定义域相同,则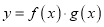 也是自倒函数.
也是自倒函数.则以上命题正确的是_______(写出所有正确命题的序号).
相关试题

