【题目】已知函数![]() ,(其中
,(其中![]() )的图象关于点
)的图象关于点![]() 成中心对称,且与点
成中心对称,且与点![]() 相邻的一个最低点为
相邻的一个最低点为![]() ,则对于下列判断:
,则对于下列判断:
①直线![]() 是函数
是函数![]() 图象的一条对称轴;
图象的一条对称轴;
②点![]() 是函数
是函数![]() 的一个对称中心;
的一个对称中心;
③函数![]() 与
与![]() 的图象的所有交点的横坐标之和为
的图象的所有交点的横坐标之和为![]() .
.
其中所有正确的判断是( )
A.①②B.①③C.②③D.②
参考答案:
【答案】C
【解析】
先根据图象关于点![]() 成中心对称,且与点
成中心对称,且与点![]() 相邻的一个最低点为
相邻的一个最低点为![]() ,分别代入求解计算出
,分别代入求解计算出![]() 的解析式,再根据三角函数的图像性质逐个判断即可.
的解析式,再根据三角函数的图像性质逐个判断即可.
因为![]() 的图象关于点
的图象关于点![]() 成中心对称,且与点
成中心对称,且与点![]() 相邻的一个最低点为
相邻的一个最低点为![]() ,故
,故![]() 且
且![]() ,故
,故![]() .所以
.所以![]() .
.
故![]() .又图像最低点为
.又图像最低点为![]() ,故
,故![]() .
.
即![]() .又
.又![]() ,故
,故![]() .故
.故![]() .
.
对①,当![]() 时
时![]() ,不是正弦函数的对称轴.故①错误.
,不是正弦函数的对称轴.故①错误.
对②,当![]() 时,
时,![]() ,故点
,故点![]() 是函数
是函数![]() 的一个对称中心,故②正确.
的一个对称中心,故②正确.
对③,因为![]() ,故
,故![]() ,所以函数
,所以函数![]() 与
与![]() 有6个交点.设交的横坐标分别为
有6个交点.设交的横坐标分别为![]() ,根据图像以及五点作图法的方法可知,当
,根据图像以及五点作图法的方法可知,当![]() 时解得
时解得![]() 为6个横坐标
为6个横坐标![]() 的对称轴.
的对称轴.
故![]() .故③正确.
.故③正确.
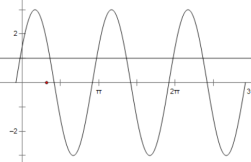
综上,②③正确.
故选:C
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
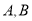 是抛物线
是抛物线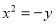 上位于
上位于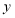 轴两侧的不同两点
轴两侧的不同两点(1)若
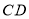 在直线
在直线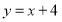 上,且使得以
上,且使得以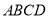 为顶点的四边形恰为正方形,求该正方形的面积.
为顶点的四边形恰为正方形,求该正方形的面积.(2)求过
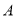 、
、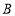 的切线与直线
的切线与直线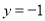 围成的三角形面积的最小值;
围成的三角形面积的最小值; -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=ex﹣ax+a(a∈R),其图象与x轴交于A(x1,0),B(x2,0)两点,且x1<x2.
(1)求a的取值范围;
(2)证明:f′(
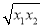 )<0(f′(x)为函数f(x)的导函数);
)<0(f′(x)为函数f(x)的导函数);(3)设点C在函数y=f(x)的图象上,且△ABC为等腰直角三角形,记
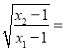 t,求(a﹣1)(t﹣1)的值.
t,求(a﹣1)(t﹣1)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解户籍、性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为200的调查样本,其中城镇户籍与农村户籍各100人;男性120人,女性80人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图,如图所示,其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
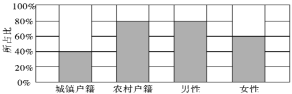
A. 是否倾向选择生育二胎与户籍有关
B. 是否倾向选择生育二胎与性别有关
C. 倾向选择生育二胎的人群中,男性人数与女性人数相同
D. 倾向选择不生育二胎的人群中,农村户籍人数少于城镇户籍人数
-
科目: 来源: 题型:
查看答案和解析>>【题目】正三棱锥
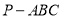 ,
,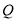 为
为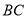 中点,
中点,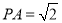 ,
,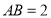 ,过
,过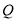 的平面截三棱锥
的平面截三棱锥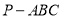 的外接球所得截面的面积范围为________.
的外接球所得截面的面积范围为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着手机的发展,“微信”逐渐成为人们支付购物的一种形式.某机构对“使用微信支付”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信支付”赞成人数如下表.
年龄
(单位:岁)
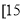 ,
,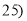
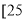 ,
,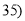
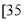 ,
,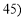
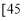 ,
,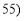
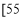 ,
,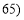
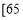 ,
,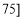
频数
5
10
15
10
5
5
赞成人数
5
10
12
7
2
1
(Ⅰ)若以“年龄45岁为分界点”,由以上计数据完成下面
 列联表,并判断是否有99%的把握认为“使用微信支付”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信支付”的态度与人的年龄有关;年龄不低于45岁的人数
年龄低于45岁的人数
合计
赞成
不赞成
合计
(Ⅱ)若从年龄在
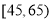 的被调查人中按照赞成与不赞成分层抽样,抽取5人进行追踪调查,在5人中抽取3人做专访,求3人中不赞成使用微信支付的人数的分布列和期望值.
的被调查人中按照赞成与不赞成分层抽样,抽取5人进行追踪调查,在5人中抽取3人做专访,求3人中不赞成使用微信支付的人数的分布列和期望值.参考数据:

0.15
0.10
0.05
0.025
0.010
0.005
0.001
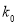
2.072
2.706
3.841
5.024
6.635
7.879
10.828
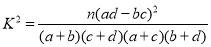 ,其中
,其中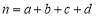 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
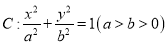 的左、右焦点分别为
的左、右焦点分别为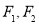 ,离心率为
,离心率为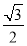 ,
,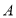 为椭圆上一动点(异于左右顶点),
为椭圆上一动点(异于左右顶点),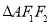 面积的最大值为
面积的最大值为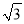 .
.(1)求椭圆
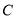 的方程;
的方程;(2)若直线
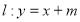 与椭圆
与椭圆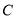 相交于点
相交于点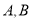 两点,问
两点,问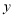 轴上是否存在点
轴上是否存在点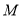 ,使得
,使得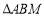 是以
是以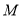 为直角顶点的等腰直角三角形?若存在,求点
为直角顶点的等腰直角三角形?若存在,求点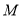 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

