【题目】已知![]() 是抛物线
是抛物线![]() 上位于
上位于![]() 轴两侧的不同两点
轴两侧的不同两点
(1)若![]() 在直线
在直线![]() 上,且使得以
上,且使得以![]() 为顶点的四边形恰为正方形,求该正方形的面积.
为顶点的四边形恰为正方形,求该正方形的面积.
(2)求过![]() 、
、![]() 的切线与直线
的切线与直线![]() 围成的三角形面积的最小值;
围成的三角形面积的最小值;
参考答案:
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]()
【解析】
(1)联解直线方程和抛物线方程,可求出![]() 的弦长
的弦长![]() ,再结合已知条件以
,再结合已知条件以![]() 为顶点的四边形为正方形可得到正方形的边长,从而可求得面积;
为顶点的四边形为正方形可得到正方形的边长,从而可求得面积;
(2)分别求出切线方程,由切线方程求出交点坐标,代入三角形的面积公式,利用基本不等式求出面积的最小值.
(1)设直线![]()
联立直线![]() 与抛物线方程得:
与抛物线方程得:![]()
易得:![]()
直线![]() 与
与![]() 之间的距离为
之间的距离为![]()
令![]() ,可得
,可得![]()
所以该正方形的边长为![]() 或
或![]()
面积为![]() 或
或![]() ;
;
(2)设![]() ,
,![]() (由对称性不妨设
(由对称性不妨设![]() )
)
则![]() 处的切线方程为:
处的切线方程为:![]() ,与直线
,与直线![]() 交点记为M,则
交点记为M,则![]()
则![]() 处的切线方程为:
处的切线方程为:![]() ,与直线
,与直线![]() 交点记为N,则
交点记为N,则![]()
两条切线交点P![]()
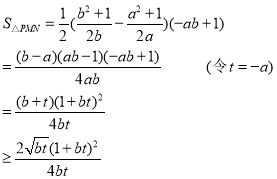
于是
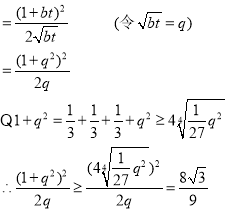
当![]() 时取到等号
时取到等号
所以该三角形面积的最小值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知动圆与
 轴相切于点
轴相切于点 ,过点
,过点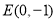 ,
,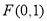 分别作动圆异于
分别作动圆异于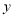 轴的两切线,设两切线相交于
轴的两切线,设两切线相交于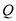 ,点
,点 的轨迹为曲线
的轨迹为曲线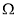 .
.(1)求曲线
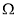 的轨迹方程;
的轨迹方程;(2)过
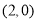 的直线
的直线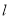 与曲线
与曲线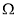 相交于不同两点
相交于不同两点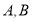 ,若曲线
,若曲线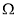 上存在点
上存在点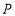 ,使得
,使得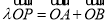 成立,求实数
成立,求实数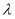 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】将字母
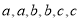 放入
放入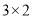 的方表格,每个格子各放一个字母,则每一行的字母互不相同,每一列的字母也互不相同的概率为_______;若共有
的方表格,每个格子各放一个字母,则每一行的字母互不相同,每一列的字母也互不相同的概率为_______;若共有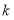 行字母相同,则得k分,则所得分数
行字母相同,则得k分,则所得分数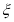 的数学期望为______;(注:横的为行,竖的为列;比如以下填法第二行的两个字母相同,第1,3行字母不同,该情况下
的数学期望为______;(注:横的为行,竖的为列;比如以下填法第二行的两个字母相同,第1,3行字母不同,该情况下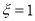 )
)a
b
c
c
a
b
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
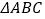 和
和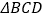 所在平面互相垂直,且
所在平面互相垂直,且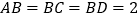 ,
,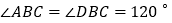 ,
,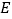 ,
,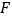 分别为
分别为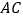 ,
,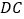 的中点.
的中点.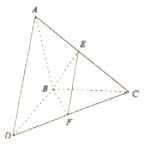
(1)求证:
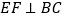 ;
;(2)求二面角
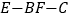 的正弦值.
的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=ex﹣ax+a(a∈R),其图象与x轴交于A(x1,0),B(x2,0)两点,且x1<x2.
(1)求a的取值范围;
(2)证明:f′(
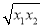 )<0(f′(x)为函数f(x)的导函数);
)<0(f′(x)为函数f(x)的导函数);(3)设点C在函数y=f(x)的图象上,且△ABC为等腰直角三角形,记
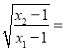 t,求(a﹣1)(t﹣1)的值.
t,求(a﹣1)(t﹣1)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解户籍、性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为200的调查样本,其中城镇户籍与农村户籍各100人;男性120人,女性80人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图,如图所示,其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
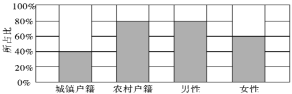
A. 是否倾向选择生育二胎与户籍有关
B. 是否倾向选择生育二胎与性别有关
C. 倾向选择生育二胎的人群中,男性人数与女性人数相同
D. 倾向选择不生育二胎的人群中,农村户籍人数少于城镇户籍人数
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
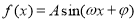 ,(其中
,(其中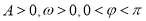 )的图象关于点
)的图象关于点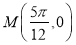 成中心对称,且与点
成中心对称,且与点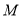 相邻的一个最低点为
相邻的一个最低点为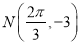 ,则对于下列判断:
,则对于下列判断:①直线
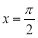 是函数
是函数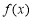 图象的一条对称轴;
图象的一条对称轴;②点
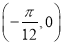 是函数
是函数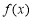 的一个对称中心;
的一个对称中心;③函数
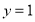 与
与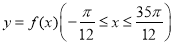 的图象的所有交点的横坐标之和为
的图象的所有交点的横坐标之和为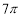 .
.其中所有正确的判断是( )
A.①②B.①③C.②③D.②
相关试题

