【题目】给定数列![]() ,若满足
,若满足![]() (
(![]() 且
且![]() ),对于任意
),对于任意![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为指数数列.
为指数数列.
(1)已知数列![]() 、
、![]() 的通项公式分别为
的通项公式分别为![]() ,
,![]() ,试判断
,试判断![]() 、
、![]() 是不是指数数列(需说明理由);
是不是指数数列(需说明理由);
(2)若数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,证明:
,证明:![]() 是指数数列;
是指数数列;
(3)若![]() 是指数数列,
是指数数列,![]() ,证明:数列
,证明:数列![]() 中任意三项都不能构成等差数列.
中任意三项都不能构成等差数列.
参考答案:
【答案】(1)![]() 不是指数数列,
不是指数数列,![]() 是指数数列,见解析;(2)见解析;(3)见解析
是指数数列,见解析;(2)见解析;(3)见解析
【解析】
(1)对数列![]() 、
、![]() ,验证
,验证![]() 与
与![]() ,
,![]() 与
与![]() 是否相等,由此判断出
是否相等,由此判断出![]() 、
、![]() 是不是指数数列.
是不是指数数列.
(2)利用累加法求得数列![]() 的通项公式,然后验证
的通项公式,然后验证![]() ,由此证得
,由此证得![]() 是指数数列.
是指数数列.
(3)首先根据指数数列的定义求得数列![]() 的通项公式,利用反证法,证得数列
的通项公式,利用反证法,证得数列![]() 中任意三项都不能构成等差数列.
中任意三项都不能构成等差数列.
(1)对于数列![]() ,
,![]() ,
,![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() 不是指数数列.
不是指数数列.
对于数列![]() ,对任意
,对任意![]() ,因为
,因为![]() ,所以
,所以![]() 是指数数列.
是指数数列.
(2)由题意,![]() ,所以数列
,所以数列![]() 是首项为
是首项为![]() ,公比为2的等比数列.所以
,公比为2的等比数列.所以![]() .
.
所以,![]()
![]() ,
,
即![]() 的通项公式为
的通项公式为![]() .所以
.所以![]() ,故
,故![]() 是指数数列.
是指数数列.
(3)因为数列![]() 是指数数列,故对于任意的
是指数数列,故对于任意的![]() ,有
,有![]() ,令
,令![]() ,则
,则![]() ,
,
所以![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,所以,
的等比数列,所以,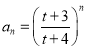 .
.
假设数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() 构成等差数列,不妨设
构成等差数列,不妨设![]() ,
,
则由![]() ,得
,得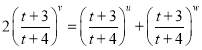 ,所以
,所以![]() ,
,
当![]() 为偶数时,
为偶数时,![]() 是偶数,而
是偶数,而![]() 是偶数,
是偶数,![]() 是奇数,
是奇数,
故![]() 不能成立;
不能成立;
当![]() 为奇数时,
为奇数时,![]() 是偶数,而
是偶数,而![]() 是奇数,
是奇数,![]() 是偶数,
是偶数,
故![]() 也不能成立.
也不能成立.
所以,对任意![]() ,
,![]() 不能成立,
不能成立,
即数列![]() 的任意三项都不成构成等差数列.
的任意三项都不成构成等差数列.
(另证:因为对任意![]() ,
,![]() 一定是偶数,而
一定是偶数,而![]() 与
与![]() 为一奇一偶,故
为一奇一偶,故![]() 与
与![]() 也为一奇一偶,故等式右边一定是奇数,等式不能成立.)
也为一奇一偶,故等式右边一定是奇数,等式不能成立.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题
①已知
 为椭圆
为椭圆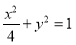 上任意一点,
上任意一点,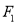 ,
,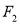 是椭圆的两个焦点,则
是椭圆的两个焦点,则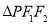 的周长是8;
的周长是8;②已知
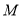 是双曲线
是双曲线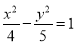 上任意一点,
上任意一点,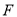 是双曲线的右焦点,则
是双曲线的右焦点,则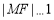 ;
;③已知直线
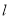 过抛物线
过抛物线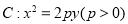 的焦点
的焦点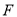 ,且
,且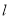 与
与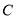 交于
交于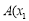 ,
,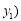 ,
, ,
,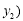 两点,则
两点,则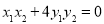 ;
;④椭圆具有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点,今有一个水平放置的椭圆形台球盘,点
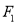 ,
,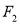 是它的焦点,长轴长为
是它的焦点,长轴长为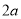 ,焦距为
,焦距为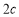 ,若静放在点
,若静放在点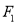 的小球(小球的半径忽略不计)从点
的小球(小球的半径忽略不计)从点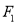 沿直线出发则经椭圆壁反射后第一次回到点
沿直线出发则经椭圆壁反射后第一次回到点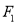 时,小球经过的路程恰好是
时,小球经过的路程恰好是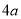 .
.其中正确命题的序号为__(请将所有正确命题的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,O为AD中点,AB=1,AD=2,AC=CD=
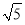 .
.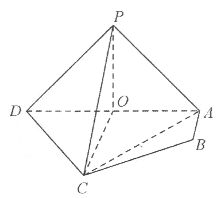
(1)证明:直线AB∥平面PCO;
(2)求二面角P-CD-A的余弦值;
(3)在棱PB上是否存在点N,使AN⊥平面PCD,若存在,求线段BN的长度;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分16分)
在平面直角坐标系xOy中,椭圆C:
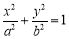 (a>b>0)的上顶点到焦点的距离为2,离心率为
(a>b>0)的上顶点到焦点的距离为2,离心率为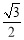 .
.(1)求a,b的值.
(2)设P是椭圆C长轴上的一个动点,过点P作斜率为k的直线l交椭圆C于A、B两点.
(ⅰ)若k=1,求△OAB面积的最大值;
(ⅱ)若PA2+PB2的值与点P的位置无关,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块长方形区域
 ,
, ,
, ,在边
,在边 的中点
的中点 处有一个可转动的探照灯,其照射角
处有一个可转动的探照灯,其照射角 始终为
始终为 ,设
,设 ,探照灯照射在长方形
,探照灯照射在长方形 内部区域的面积为
内部区域的面积为 .
.(1)求
 关于
关于 的函数关系式;
的函数关系式;(2)当
 时,求
时,求 的最大值.
的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
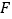 为抛物线
为抛物线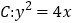 的焦点,过点
的焦点,过点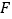 的直线
的直线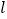 与抛物线
与抛物线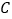 相交于
相交于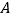 、
、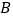 两点.
两点.(1)若
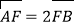 ,求此时直线
,求此时直线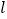 的方程;
的方程;(2)若与直线
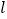 垂直的直线
垂直的直线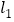 过点
过点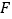 ,且与抛物线
,且与抛物线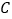 相交于点
相交于点 、
、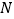 ,设线段
,设线段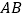 、
、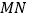 的中点分别为
的中点分别为 、
、 ,如图,求证:直线
,如图,求证:直线 过定点;
过定点;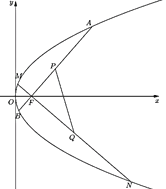
(3)设抛物线
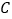 上的点
上的点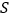 、
、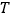 在其准线上的射影分别为
在其准线上的射影分别为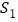 、
、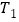 ,若△
,若△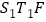 的面积是△
的面积是△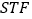 的面积的两倍,如图,求线段
的面积的两倍,如图,求线段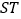 中点的轨迹方程.
中点的轨迹方程.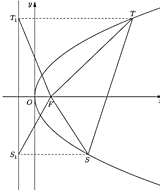
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四个关于圆锥曲线的命题中
①设A.B为两个定点,k为非零常数,
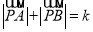 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;②曲线
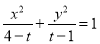 表示焦点在y轴上的椭圆,则
表示焦点在y轴上的椭圆,则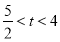 ;
;③方程
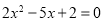 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;④双曲
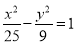 与椭圆
与椭圆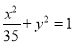 有相同的焦点.
有相同的焦点.其中真命题的序号( )
A.②③④B.①②③C.①③④D.①②④
相关试题

