【题目】如图,一块长方形区域![]() ,
,![]() ,
,![]() ,在边
,在边![]() 的中点
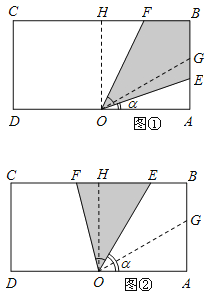
的中点![]() 处有一个可转动的探照灯,其照射角
处有一个可转动的探照灯,其照射角![]() 始终为
始终为![]() ,设
,设![]() ,探照灯照射在长方形
,探照灯照射在长方形![]() 内部区域的面积为
内部区域的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,求
时,求![]() 的最大值.
的最大值.

参考答案:
【答案】(1)S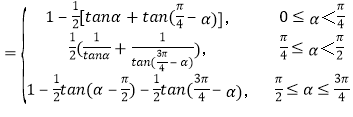 (2)
(2)![]()
【解析】
(1)根据条件讨论α的范围,结合三角形的面积公式进行求解即可.
(2)利用两角和差的三角公式进行化简,结合基本不等式的性质进行转化求解即可.
(1)![]() ,
,
则OA=1,即AE=tanα,
∠HOF![]() α,
α,
HF=tan(![]() α),
α),
则△AOE,△HOF得面积分别为![]() tanα
tanα![]() ,
,![]() tan(
tan(![]() α)
α)![]() ,
,
则阴影部分的面积S=1![]() ,
,![]() ,
,
当∈[![]() ,
,![]() )时,E在BH上,F在线段CH上,如图②,
)时,E在BH上,F在线段CH上,如图②,
EH![]() ,FH
,FH![]() ,则EF
,则EF![]() ,
,
则S![]() (
(![]() ),
),
即![]() ,
,![]() ;
;
同理当![]() ,
,![]() ;
;
即S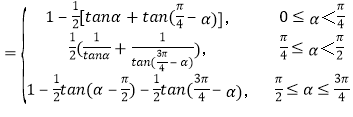 .
.
(2)当![]() 时,S=1
时,S=1![]() 2
2![]() (1+tanα
(1+tanα![]() )
)
∵0≤tanα≤1,即1≤1+tanα≤2,
则1+tanα![]() 2
2![]() 2
2![]() ,
,
当且仅当1+tanα![]() ,即1+tanα
,即1+tanα![]() 时取等号,
时取等号,
即![]() ,即S的最大值为2
,即S的最大值为2![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
 是边长为3的正方形,
是边长为3的正方形,  平面
平面 与平面
与平面 所成角为
所成角为 .
.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)设点
 是线段
是线段 上一个动点,试确定点
上一个动点,试确定点 的位置,使得
的位置,使得 平面
平面 ,并证明你的结论.
,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】某研究性学习小组为了调查研究学生玩手机对学习的影响,现抽取了30名学生,得到数据如表:
玩手机
不玩手机
合计
学习成绩优秀
8
学习成绩不优秀
16
合计
30
已知在全部的30人中随机抽取1人,抽到不玩手机的概率为
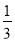 .
.(1)请将2×2列联表补充完整;
(2)能否在犯错误的概率不超过0.005的前提下认为玩手机对学习有影响;
(3)现从不玩手机,学习成绩优秀的8名学生中任意选取两人,对他们的学习情况进行全程跟踪,记甲、乙两名学生被抽到的人数为X,求X的分布列和数学期望.
附:
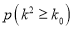
0.15
0.10
0.05
0.025
0.010
0.005
0.001
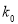
2.072
2.706
3.841
5.024
6.635
7.879
10.828
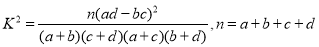 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.

(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的
 列联表,据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
列联表,据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?优秀
合格
合计
大学组
中学组
合计
注:
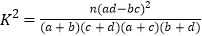 ,其中
,其中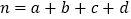 .
.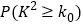
0.10
0.05
0.005
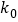
2.706
3.841
7.879
(2)若参赛选手共6万人,用频率估计概率,试估计其中优秀等级的选手人数.
(3)在优秀等级的选手中取6名,依次编号为1,2,3,4,5,6.在良好等级的选手中取6名,依次编号为1,2,3,4,5,6,在选出的6名优秀等级的选手中任取一名,记其编号为

,在选出的6名良好等级的选手中任取一名,记其编号为 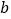 ,求使得方程组
,求使得方程组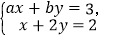 有唯一一组实数解
有唯一一组实数解 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

 .
.(1)若曲线
 在
在 处切线的斜率为
处切线的斜率为 ,求此切线方程;
,求此切线方程;(2)若
 有两个极值点
有两个极值点 ,求
,求 的取值范围,并证明:
的取值范围,并证明: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学在研究函数

 时,给出下面几个结论中正确的有( )
时,给出下面几个结论中正确的有( )A.
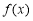 的图象关于点
的图象关于点 对称B.若
对称B.若 ,则
,则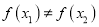
C.
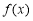 的值域为
的值域为 D.函数
D.函数 有三个零点
有三个零点 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分14分)如图,已知椭圆
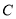 :
: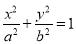 ,其左右焦点为
,其左右焦点为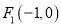 及
及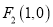 ,过点
,过点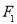 的直线交椭圆
的直线交椭圆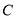 于
于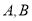 两点,线段
两点,线段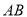 的中点为
的中点为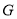 ,
,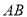 的中垂线与
的中垂线与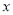 轴和
轴和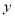 轴分别交于
轴分别交于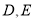 两点,且
两点,且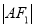 、
、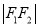 、
、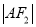 构成等差数列.
构成等差数列.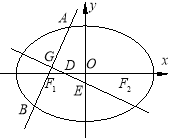
(1)求椭圆
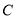 的方程;
的方程;(2)记△
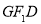 的面积为
的面积为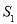 ,△
,△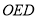 (
(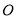 为原点)的面积为
为原点)的面积为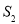 .试问:是否存在直线
.试问:是否存在直线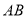 ,使得
,使得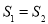 ?说明理由.
?说明理由.
相关试题

