【题目】设![]() 为抛物线
为抛物线![]() 的焦点,过点
的焦点,过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)若![]() ,求此时直线
,求此时直线![]() 的方程;
的方程;
(2)若与直线![]() 垂直的直线
垂直的直线![]() 过点
过点![]() ,且与抛物线
,且与抛物线![]() 相交于点
相交于点![]() 、
、![]() ,设线段
,设线段![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() ,如图,求证:直线
,如图,求证:直线![]() 过定点;
过定点;
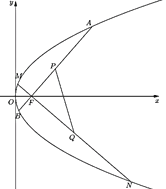
(3)设抛物线![]() 上的点
上的点![]() 、
、![]() 在其准线上的射影分别为
在其准线上的射影分别为![]() 、
、![]() ,若△
,若△![]() 的面积是△
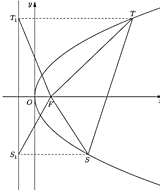
的面积是△![]() 的面积的两倍,如图,求线段
的面积的两倍,如图,求线段![]() 中点的轨迹方程.
中点的轨迹方程.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)求出抛物线的焦点坐标,由直线方程的点斜式写出直线l的方程,和抛物线方程联立后利用![]() 2
2![]() 得直线
得直线![]() 方程.
方程.
(2由(1)得点P![]() ,又直线
,又直线![]() 与直线
与直线![]() 垂直,将m换为
垂直,将m换为![]() ,同理可得Q(
,同理可得Q(![]() ,﹣
,﹣![]() ).由此可求直线PQ的方程,可得结论;
).由此可求直线PQ的方程,可得结论;
(3)利用△![]() 的面积是△
的面积是△![]() 的面积的两倍,求出N的坐标,再利用直线的斜率公式及点差法求TS中点的轨迹方程.
的面积的两倍,求出N的坐标,再利用直线的斜率公式及点差法求TS中点的轨迹方程.
(1)抛物线焦点坐标为F(1,0),设直线![]() 方程为x=my+1,
方程为x=my+1,
设点A(x1,y1),B(x2,y2),
联立![]() ,得:y2﹣4my﹣4=0,
,得:y2﹣4my﹣4=0,
则由韦达定理有:y1+y2=4m,①,y1y2=﹣4,②
∵![]() 2
2![]() ,
,
∴1﹣x1=2(x2﹣1),﹣y1=2y2,③,
由①②③可得m2![]() ,∴
,∴![]() ,
,
∴直线方程为x=![]() y+1,即
y+1,即![]() .
.
(2)由(1)得点P![]() ,又直线
,又直线![]() 与直线
与直线![]() 垂直,将m换为
垂直,将m换为![]() ,
,
同理可得Q(![]() ,﹣
,﹣![]() ).
).
m![]() 时,直线PQ的斜率kPQ
时,直线PQ的斜率kPQ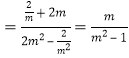 ,
,
直线PQ的方程为:y-2m![]() (x﹣1﹣2
(x﹣1﹣2![]() ),整理为m(x﹣3)﹣(m2﹣1)y=0,于是直线PQ恒过定点E(3,0),
),整理为m(x﹣3)﹣(m2﹣1)y=0,于是直线PQ恒过定点E(3,0),
m=±1时,直线PQ的方程为:x=3,也经过点E(3,0).
综上所述:直线PQ恒过定点E(3,0).
(3)设S(x1,y1),T(x2,y2),
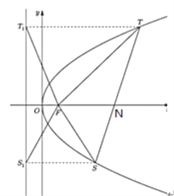
F(1,0),准线为 x=﹣1,![]() 2|
2|![]() |=|y1﹣y2|,
|=|y1﹣y2|,
设直线TS与x轴交点为N,
∴S△TSF![]() |FN||y1﹣y2|,
|FN||y1﹣y2|,
∵![]() 的面积是△TSF的面积的两倍,
的面积是△TSF的面积的两倍,
∴![]() |FN|=
|FN|=![]() ,∴|FN|=1,
,∴|FN|=1,
∴xN=2,即N(2,0).
设TS中点为M(x,y),由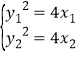 span>得
span>得![]() ﹣
﹣![]() =4(x1﹣x2),
=4(x1﹣x2),
又![]() ,
,
∴![]() ,即y2=2x﹣4.
,即y2=2x﹣4.
∴TS中点轨迹方程为y2=2x﹣4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分16分)
在平面直角坐标系xOy中,椭圆C:
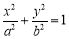 (a>b>0)的上顶点到焦点的距离为2,离心率为
(a>b>0)的上顶点到焦点的距离为2,离心率为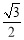 .
.(1)求a,b的值.
(2)设P是椭圆C长轴上的一个动点,过点P作斜率为k的直线l交椭圆C于A、B两点.
(ⅰ)若k=1,求△OAB面积的最大值;
(ⅱ)若PA2+PB2的值与点P的位置无关,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给定数列
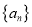 ,若满足
,若满足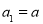 (
(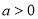 且
且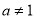 ),对于任意
),对于任意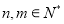 ,都有
,都有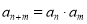 ,则称数列
,则称数列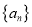 为指数数列.
为指数数列.(1)已知数列
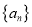 、
、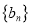 的通项公式分别为
的通项公式分别为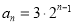 ,
,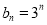 ,试判断
,试判断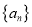 、
、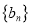 是不是指数数列(需说明理由);
是不是指数数列(需说明理由);(2)若数列
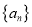 满足:
满足: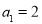 ,
,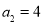 ,
,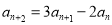 ,证明:
,证明: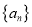 是指数数列;
是指数数列;(3)若
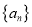 是指数数列,
是指数数列,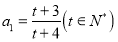 ,证明:数列
,证明:数列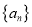 中任意三项都不能构成等差数列.
中任意三项都不能构成等差数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块长方形区域
 ,
, ,
, ,在边
,在边 的中点
的中点 处有一个可转动的探照灯,其照射角
处有一个可转动的探照灯,其照射角 始终为
始终为 ,设
,设 ,探照灯照射在长方形
,探照灯照射在长方形 内部区域的面积为
内部区域的面积为 .
.(1)求
 关于
关于 的函数关系式;
的函数关系式;(2)当
 时,求
时,求 的最大值.
的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四个关于圆锥曲线的命题中
①设A.B为两个定点,k为非零常数,
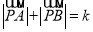 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;②曲线
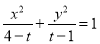 表示焦点在y轴上的椭圆,则
表示焦点在y轴上的椭圆,则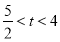 ;
;③方程
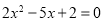 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;④双曲
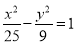 与椭圆
与椭圆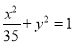 有相同的焦点.
有相同的焦点.其中真命题的序号( )
A.②③④B.①②③C.①③④D.①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】设各项均为正数的数列
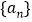 的前
的前 项和为
项和为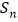 ,且
,且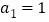 ,
,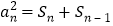 (
(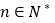 ,
, ),数列
),数列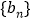 满足
满足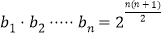 (
(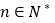 ).
).(1)求数列
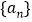 、
、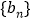 的通项公式;
的通项公式;(2)设
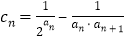 ,
, 是
是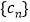 的前
的前 项和,求正整数
项和,求正整数 ,使得对任意的
,使得对任意的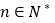 ,
,均有
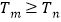 ;
;(3)设
 ,且
,且 ,其中
,其中 (
(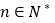 ,
, ),求集合
),求集合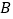 中所有元素的和.
中所有元素的和. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据下图给出的2000年至2016年我国实际利用外资情况,以下结论正确的是

A. 2000年以来我国实际利用外资规模与年份负相关
B. 2010年以来我国实际利用外资规模逐年增加
C. 2008年我国实际利用外资同比增速最大
D. 2010年以来我国实际利用外资同比增速最大
相关试题

