【题目】我们用圆的性质类比球的性质如下:
①p:圆心与弦(非直径)中点的连线垂直于弦; q:球心与小圆截面圆心的连线垂直于截面.
②p:与圆心距离相等的两条弦长相等; q:与球心距离相等的两个截面圆的面积相等.
③p:圆的周长为C=πd(d是圆的直径); q:球的表面积为S=πd2(d是球的直径).
④p:圆的面积为S=![]() R·πd(R,d是圆的半径与直径); q:球的体积为V=
R·πd(R,d是圆的半径与直径); q:球的体积为V=![]() R·πd2(R,d是球的半径与直径).
R·πd2(R,d是球的半径与直径).
则上面的四组命题中,其中类比得到的q是真命题的有( )个
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】D
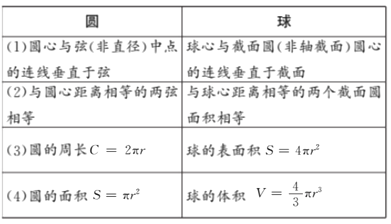
【解析】圆与球有以下类似的性质:
(1)圆是平面上一点的距离等于定长的所有点构成的集合,球面是空间中到一定点的距离等于定长的所有点构成的集合.
(2)圆是平面内封闭的曲线所围成的对称图形,球是空间中封闭的曲面所围成的对称图形.
与圆的有关性质相比较,可以推测球的有关性质:
结合题意可知所给的选项都是正确的.
本题选择D选项.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
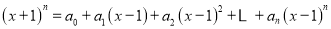 ,(其中
,(其中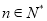 ).
).(1)求
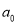 及
及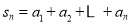 ;
;(2)试比较
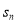 与
与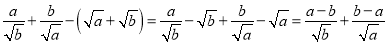 的大小,并用数学归纳法给出证明过程.
的大小,并用数学归纳法给出证明过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生身高情况,某校以
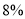 的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为
的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为 ,测得男生身高情况的频率分布直方图(如图所示):
,测得男生身高情况的频率分布直方图(如图所示):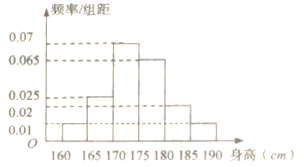
(1)计算所抽取的男生人数,并估计男生身高的中位数(保留两位小数);
(2)从样本中身高在
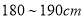 之间的男生中任选2人,求至少有1人身高在
之间的男生中任选2人,求至少有1人身高在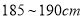 之间的概率.
之间的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
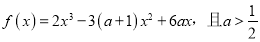 .
.(I)若函数
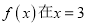 处取得极值,求曲线
处取得极值,求曲线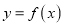 在点
在点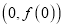 处的切线方程;
处的切线方程;(II)若函数
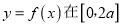 上的最小值是
上的最小值是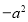 ,求
,求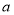 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=ex﹣ax2,曲线y=f(x)在(1,f(1))处的切线方程为y=bx+1.
(1)求a,b的值;
(2)求f(x)在[0,1]上的最大值;
(3)证明:当x>0时,ex+(1﹣e)x﹣xlnx﹣1≥0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为圆O的直径,点E,F在圆O上,且AB//EF,AB=2EF,矩形ABCD所在的平面和圆O所在的平面互相垂直.
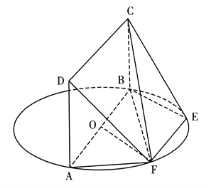
(I)证明:OF//平面BEC;
(Ⅱ)证明:平面ADF
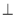 平面BCF.
平面BCF. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位射击运动员,在某天训练中已各射击10次,每次命中的环数如下:
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
(Ⅰ)通过计算估计,甲、乙二人的射击成绩谁更稳;
(Ⅱ)若规定命中8环及以上环数为优秀,以频率作为概率,请依据上述数据估计,求甲在第11至第13次射击中获得优秀的次数
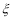 的分布列和期望.
的分布列和期望.
相关试题

