【题目】为了解学生身高情况,某校以![]() 的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为
的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为![]() ,测得男生身高情况的频率分布直方图(如图所示):
,测得男生身高情况的频率分布直方图(如图所示):
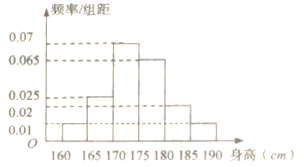
(1)计算所抽取的男生人数,并估计男生身高的中位数(保留两位小数);
(2)从样本中身高在![]() 之间的男生中任选2人,求至少有1人身高在
之间的男生中任选2人,求至少有1人身高在![]() 之间的概率.
之间的概率.
参考答案:
【答案】(1)174.64cm(2)![]() .
.
【解析】试题分析:
(1)由题意结合中位数的求法可得男生身高的中位数是174.64cm;
(2)列出所有可能的事件,结合古典概型公式可得至少有1人身高在![]() 之间的概率是
之间的概率是![]() .
.
试题解析:
(1)由题意得,所抽取的男生人数为:
1000×8%×![]() =40人
=40人
依据样本频率分布直方图:0.01×5+0.025×5+x=0.5 得x=0.325 ,而身高170~175之间的频率为0.35,所以中位数为170+5×![]() ≈174.64cm
≈174.64cm
(2)样本中身高在180~185 cm之间的男生有4人,设其编号为①,②,③,④,样本中身高在185~190 cm之间的男生有2人,设其编号为⑤,⑥,从上述6人中任取2人的共有:
(①,②)(①,③)(①,④)(①,⑤)(①,⑥)
(②,③)(②,④)(②,⑤)(②,⑥)
(③,④)(③,⑤)(③,⑥)
(④,⑤)(④,⑥)
(⑤,⑥)
故从样本中身高在180~190 cm之间的男生中任选2人的所有可能结果数为15,至少有1人身高在185~190 cm之间的可能结果数为9,因此,所求概率P2=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】葫芦岛市某高中进行一项调查:2012年至2016年本校学生人均年求学花销
 (单位:万元)的数据如下表:
(单位:万元)的数据如下表:年份
2012
2013
2014
2015
2016
年份代号
1
2
3
4
5
年求学花销
3.2
3.5
3.8
4.6
4.9
(1)求
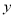 关于
关于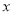 的线性回归方程;
的线性回归方程;(2)利用(1)中的回归方程,分析2012年至2016年本校学生人均年求学花销的变化情况,并预测该地区2017年本校学生人均年求学花销情况.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
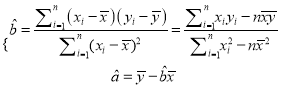
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a∈R,函数
 .
.(I)若函数
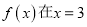 处取得极值,求曲线
处取得极值,求曲线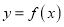 在点
在点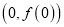 处的切线方程;
处的切线方程;(Ⅱ)若
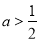 ,函数
,函数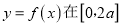 上的最小值是
上的最小值是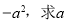 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
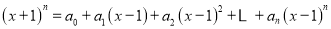 ,(其中
,(其中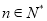 ).
).(1)求
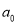 及
及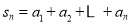 ;
;(2)试比较
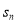 与
与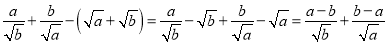 的大小,并用数学归纳法给出证明过程.
的大小,并用数学归纳法给出证明过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
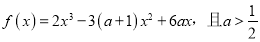 .
.(I)若函数
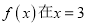 处取得极值,求曲线
处取得极值,求曲线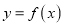 在点
在点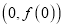 处的切线方程;
处的切线方程;(II)若函数
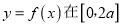 上的最小值是
上的最小值是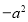 ,求
,求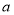 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们用圆的性质类比球的性质如下:
①p:圆心与弦(非直径)中点的连线垂直于弦; q:球心与小圆截面圆心的连线垂直于截面.
②p:与圆心距离相等的两条弦长相等; q:与球心距离相等的两个截面圆的面积相等.
③p:圆的周长为C=πd(d是圆的直径); q:球的表面积为S=πd2(d是球的直径).
④p:圆的面积为S=
 R·πd(R,d是圆的半径与直径); q:球的体积为V=
R·πd(R,d是圆的半径与直径); q:球的体积为V= R·πd2(R,d是球的半径与直径).
R·πd2(R,d是球的半径与直径).则上面的四组命题中,其中类比得到的q是真命题的有( )个
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=ex﹣ax2,曲线y=f(x)在(1,f(1))处的切线方程为y=bx+1.
(1)求a,b的值;
(2)求f(x)在[0,1]上的最大值;
(3)证明:当x>0时,ex+(1﹣e)x﹣xlnx﹣1≥0.
相关试题

