【题目】已知函数，，若函数有3个不同的零点x1，x2，x3(x1＜x2＜x3)，则的取值范围是_________．

【答案】

【解析】

先根据题意，求出的解得或，然后求出f(x)的导函数，求其单调性以及最值，在根据题意求出函数有3个不同的零点x1，x2，x3(x1＜x2＜x3)，分情况讨论求出的取值范围.

解：令t=f（x），函数有3个不同的零点，

即+m=0有两个不同的解，解之得

即或

因为的导函数

，令，解得x>e，，解得0<x<e，

可得f（x）在（0，e）递增，在递减；

f(x)的最大值为 ，且

且f(1)=0；

要使函数有3个不同的零点，

（1）有两个不同的解，此时有一个解；

（2）有两个不同的解，此时有一个解

当有两个不同的解，此时有一个解，

此时 ，不符合题意；

或是不符合题意；

所以只能是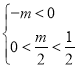 解得

，

此时=-m，

此时

有两个不同的解，此时有一个解

此时 ，不符合题意；

或是不符合题意；

所以只能是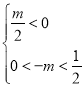解得

，

此时=，

综上：的取值范围是

故答案为

关闭