搜索
【题目】已知双曲线
的左、右焦点分别为
，圆
与双曲线在第一象限内的交点为M，若
．则该双曲线的离心率为
A. 2B. 3C. 
D. 
【答案】D
【解析】
本题首先可以通过题意画出图像并过
点作
垂线交于点
，然后通过圆与双曲线的相关性质判断出三角形
的形状并求出高
的长度，的长度即点纵坐标，然后将点纵坐标带入圆的方程即可得出点坐标，最后将点坐标带入双曲线方程即可得出结果。
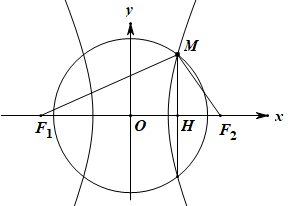
根据题意可画出以上图像，过点作垂线并交于点，
因为
，在双曲线上，
所以根据双曲线性质可知，
，即
，
，
因为圆
的半径为
，
是圆的半径，所以
，
因为，，
，
，
所以
，三角形是直角三角形，
因为
，所以
，
，即点纵坐标为
，
将点纵坐标带入圆的方程中可得
，解得
，
，
将点坐标带入双曲线中可得
，
化简得
，
，
，
，故选D。
