【题目】已知f(x)=|x﹣2|+|x+1|+2|x+2|.
(Ⅰ)求证:f(x)≥5;
(Ⅱ)若对任意实数x,15﹣2f(x)<a2+ ![]() 都成立,求实数a的取值范围.
都成立,求实数a的取值范围.
参考答案:
【答案】证明:(Ⅰ)∵  , ∴f(x)的最小值为5,∴f(x)≥5.
, ∴f(x)的最小值为5,∴f(x)≥5.
(Ⅱ)解:由(Ⅰ)知:15﹣2f(x)的最大值等于5.
∵ ![]() ,
,
“=”成立 ![]() ,即
,即 ![]() ,
,
∴当 ![]() 时,
时, ![]() 取得最小值5.
取得最小值5.
当 ![]() 时,
时, ![]() ,
,
又∵对任意实数x, ![]() 都成立,
都成立,
∴ ![]() .∴a的取值范围为
.∴a的取值范围为 ![]()
【解析】(Ⅰ)通过讨论x的范围,得到关于f(x)的分段函数,从而求出f(x)的最小值即可;(Ⅱ)根据基本不等式的性质求出a的范围即可.
【考点精析】本题主要考查了绝对值不等式的解法的相关知识点,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
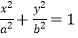 (a>b>0)的离心率为
(a>b>0)的离心率为  ,直线l:y=x+2与以原点为圆心、椭圆C的短半轴为半径的圆O相切.
,直线l:y=x+2与以原点为圆心、椭圆C的短半轴为半径的圆O相切.
(1)求椭圆C的方程;
(2)过椭圆C的左顶点A作直线m,与圆O相交于两点R,S,若△ORS是钝角三角形,求直线m的斜率k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数h(x)=lnx+
 .
.
(1)函数g(x)=h(2x+m),若x=1是g(x)的极值点,求m的值并讨论g(x)的单调性;
(2)函数φ(x)=h(x)﹣ +ax2﹣2x有两个不同的极值点,其极小值为M,试比较2M与﹣3的大小关系,并说明理由.
+ax2﹣2x有两个不同的极值点,其极小值为M,试比较2M与﹣3的大小关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面直角坐标系xOy中,以O为极点,x轴的非负半轴为极轴建立极坐标系,P点的极坐标为(3,
 ).曲线C的参数方程为ρ=2cos(θ﹣
).曲线C的参数方程为ρ=2cos(θ﹣  )(θ为参数).
)(θ为参数).
(Ⅰ)写出点P的直角坐标及曲线C的直角坐标方程;
(Ⅱ)若Q为曲线C上的动点,求PQ的中点M到直线l:2ρcosθ+4ρsinθ= 的距离的最小值.
的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若偶函数f(x)在(﹣∞,0]上单调递减,a=f(log23),b=f(log45),c=f(2
 ),则a,b,c满足( )
),则a,b,c满足( )
A.a<b<c
B.b<a<c
C.c<a<b
D.c<b<a -
科目: 来源: 题型:
查看答案和解析>>【题目】计算机在数据处理时使用的是二进制,例如十进制的1、2、3、4在二进制分别表示为1、10、11、100.下面是某同学设计的将二进制数11111化为十进制数的一个流程图,则判断框内应填入的条件是( )

A.i>4
B.i≤4
C.i>5
D.i≤5 -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,
, 与
与 是
是 的子集,若
的子集,若 ,则称
,则称 为一个“理想配集”,那么符合此条件的“理想配集”的个数是________.(规定
为一个“理想配集”,那么符合此条件的“理想配集”的个数是________.(规定 与
与 是两个不同的“理想配集”)
是两个不同的“理想配集”)
相关试题

