【题目】在△ABC中,角A,B的对边分别为a,b,根据下列条件解三角形,其中只有一解的为( )
A.a=50,b=30,A=60°B.a=30,b=65,A=30°
C.a=30,b=50,A=30°D.a=30,b=60,A=30°
参考答案:
【答案】AD
【解析】
由已知结合正弦定理求解sinB,再由正弦函数的值域及三角形中大边对大角分析得答案.
对于A,由a=50,b=30,A=60°,
利用正弦定理可得:![]()
则sinB![]() ,
,
∵a>b,且A为锐角,∴B有一解,故三角形只有一解;
对于B,由a=30,b=65,A=30°,
利用正弦定理可得:![]()
则sinB![]() ,此三角形无解;
,此三角形无解;
对于C,由a=30,b=50,A=30°,
利用正弦定理可得:![]()
则sinB![]() ,
,
∵b>a,且A为锐角,则角B有两解,故三角形有两解;
对于D,由a=30,b=60,A=30°,
利用正弦定理可得:![]() ,
,
则sinB=1,B=90°,三角形为直角三角形,仅有一解.
故选:AD
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂要建造一个长方形无盖蓄水池,其容积为
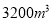 立方米,深为
立方米,深为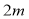 .如果池底每平方米的造价为
.如果池底每平方米的造价为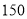 元,池壁每平方米的造价为
元,池壁每平方米的造价为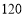 元,那么怎样设计水池能使总造价最低(设蓄水池池底的相邻两边边长分别为
元,那么怎样设计水池能使总造价最低(设蓄水池池底的相邻两边边长分别为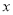 ,
,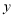 )?最低总造价是多少?
)?最低总造价是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】设
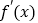 是定义域为
是定义域为 的函数
的函数 的导函数,
的导函数, ,
, ,则
,则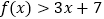 的解集为( )
的解集为( )A.
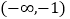 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆的中心在原点,焦点在
 轴上,长轴长是短轴长的2倍且经过点
轴上,长轴长是短轴长的2倍且经过点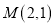 ,平行于
,平行于 的直线
的直线 在
在 轴上的截距为
轴上的截距为 ,直线
,直线 交椭圆于
交椭圆于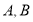 两个不同点.
两个不同点.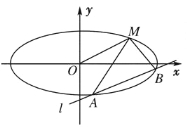
(1)求椭圆的方程;
(2)求
 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆M:
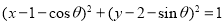 ,直线l:
,直线l: ,下列四个选项,其中正确的是( )
,下列四个选项,其中正确的是( )A.对任意实数k与θ,直线l和圆M有公共点
B.存在实数k与θ,直线l和圆M相离
C.对任意实数k,必存在实数θ,使得直线l与圆M相切
D.对任意实数θ,必存在实数k,使得直线l与圆M相切
-
科目: 来源: 题型:
查看答案和解析>>【题目】解关于x的不等式

-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,
, 是双曲线C:
是双曲线C: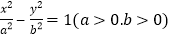 的左,右焦点,O是坐标原点
的左,右焦点,O是坐标原点 过
过 作C的一条渐近线的垂线,垂足为P,若
作C的一条渐近线的垂线,垂足为P,若 ,则C的离心率为
,则C的离心率为

A.
 B. 2 C.
B. 2 C.  D.
D. 
相关试题

