【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)先求函数的定义域,求导通分后发现分母是含有参数的二次函数,根据其判别式进行分类讨论,由此求得函数的单调区间.(2)将![]() 和
和![]() 代入原函数,可将原不等式化简为
代入原函数,可将原不等式化简为![]() 恒成立,利用分离常数法,可将问题转化为切线的斜率来求解.
恒成立,利用分离常数法,可将问题转化为切线的斜率来求解.
试题解析:(1)![]() ,
,
令![]() ,判别式为:
,判别式为:![]() ,
,
①:当![]() ,得
,得![]() ,
,
此时![]() ,从而
,从而![]() ,
,
所以![]() 在
在![]() 上单调递增.
上单调递增.
②:当![]() ,即
,即![]() ,
,
令![]() ,得方程的根
,得方程的根
![]() (舍去),
(舍去),![]() ,
,
若![]() ,此时
,此时![]() ,
,![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 单调递减,
单调递减,
若![]() ,此时
,此时![]() 的对称轴为
的对称轴为![]() ,
,
![]() ,
,
∴![]() ,从而
,从而![]() 在
在![]() 上单调递增.
上单调递增.
综上:当![]() ,
,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]() 单调递减.
单调递减.
(2)由题意有![]() 恒成立,
恒成立,
即![]() ,
,
即![]() 恒成立,
恒成立,
当![]() 时,不等式显然恒成立,
时,不等式显然恒成立,
当![]() 时,
时,![]() ,
,
所以![]() ,则
,则![]() ,于是
,于是
![]() ,在
,在![]() 上恒成立,
上恒成立,
令![]() ,
,
设![]() ,
,![]() ,
,
则![]() ,且
,且![]() 两点在
两点在![]() 的图象上,
的图象上,
又![]() ,
,
故![]() ,
,
所以![]() ,
,
故![]() 为所求.
为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的右焦点
的右焦点 ,椭圆
,椭圆 的左,右顶点分别为
的左,右顶点分别为 .过点
.过点 的直线
的直线 与椭圆交于
与椭圆交于 两点,且
两点,且 的面积是
的面积是 的面积的3倍.
的面积的3倍. (Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)若
 与
与 轴垂直,
轴垂直, 是椭圆
是椭圆 上位于直线
上位于直线 两侧的动点,且满足
两侧的动点,且满足 ,试问直线
,试问直线 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品在
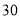 天每件的销售价格
天每件的销售价格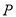 (元)与时间
(元)与时间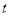 (天)的函数关系用如图表示,该商品在
(天)的函数关系用如图表示,该商品在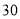 天内日销售量
天内日销售量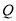 (件)与时间
(件)与时间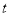 (天)之间的关系如下表:
(天)之间的关系如下表: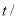 天
天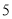
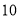
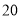
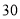
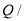 件
件

(
 )根据提供的图象(如图),写出该商品每件的销售价格
)根据提供的图象(如图),写出该商品每件的销售价格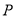 与时间
与时间 的函数关系式.
的函数关系式.(
 )根据表
)根据表 提供的数据,写出日销售量
提供的数据,写出日销售量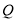 与时间
与时间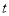 的一次函数关系式.
的一次函数关系式.(
 )求该商品的日销售金额的最大值,并指出日销售金额最大的一天是
)求该商品的日销售金额的最大值,并指出日销售金额最大的一天是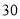 天中的第几天.(日销售金额
天中的第几天.(日销售金额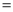 每件的销售价格
每件的销售价格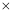 日销售量)
日销售量) -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
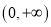 上的函数
上的函数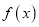 ,如果对任意的
,如果对任意的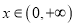 ,都有
,都有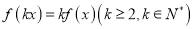 成立,则称
成立,则称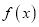 为
为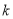 阶伸缩函数.
阶伸缩函数.(
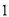 )若函数
)若函数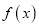 为二阶伸缩函数,且当
为二阶伸缩函数,且当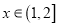 时,
时, 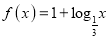 ,求
,求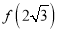 的值.
的值.(
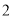 )若
)若 为三阶伸缩函数,且当
为三阶伸缩函数,且当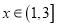 时,
时, 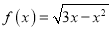 ,求证:函数
,求证:函数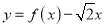 在
在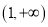 上无零点.
上无零点.(
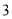 )若函数
)若函数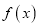 为
为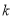 阶伸缩函数,且当
阶伸缩函数,且当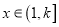 时,
时, 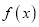 的取值范围是
的取值范围是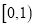 ,求
,求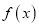 在
在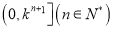 上的取值范围.
上的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出四种说法:
①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
②命题P:“x0∈R,x02﹣x0﹣1>0”的否定是¬P:“x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(x>1)=p则P(﹣1<X<0)=
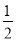 ﹣p
﹣p④回归直线一定过样本点的中心(
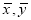 ).
).其中正确的说法有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
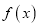 ,若存在实数对(
,若存在实数对(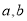 ),使得等式
),使得等式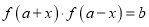 对定义域中的每一个
对定义域中的每一个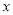 都成立,则称函数
都成立,则称函数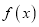 是“(
是“(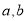 )型函数”.
)型函数”.(1) 判断函数
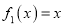 是否为 “(
是否为 “(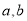 )型函数”,并说明理由;
)型函数”,并说明理由;(2) 若函数
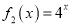 是“(
是“(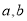 )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对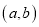 ;
;(3)已知函数
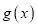 是“(
是“(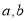 )型函数”,对应的实数对
)型函数”,对应的实数对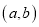 为(1,4).当
为(1,4).当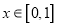 时,
时, 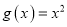
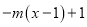
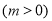 ,若当
,若当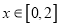 时,都有
时,都有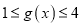 ,试求
,试求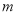 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋中有7个大小、形状相同的小球,6个白球1个红球.现任取1个,若为红球就停止,若为白球就放回,搅拌均匀后再接着取.试设计一个模拟试验,计算恰好第三次摸到红球的概率.
相关试题

