【题目】如图,在直三棱柱ABC﹣A1B1C1中,D为AC的中点,∠ABC=90°,AA1=AB=2,BC=3. 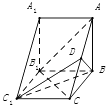
(1)求证:AB1∥平面BC1D;
(2)求三棱锥D﹣BC1C的体积.
参考答案:
【答案】
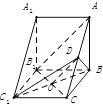
(1)证明:设B1C与BC1相交于点O,连接OD.
∵四边形BCC1B1是平行四边形
∴点O为B1C的中点,又D为AC的中点
∴OD∥AB1.
∵OD平面BC1D,AB1平面BC1D
∴AB1∥平面BC1D
(2)解:在直三棱柱ABCA1B1C1中,侧棱CC1⊥平面ABC
故CC1为三棱锥C1﹣BCD的高,CC1=A1A=2.
∵D为AC的中点,∠ABC=90°
∴S△BCD= ![]() S△ABC=
S△ABC= ![]() ×(
×( ![]() BC×AB)=
BC×AB)= ![]() .
.
∴VD﹣BC1C=VC1﹣BCD= ![]() S△BCDCC1=
S△BCDCC1= ![]() ×
× ![]() ×2=1.
×2=1.
【解析】(1)设B1C与BC1相交于点O,连接OD,则由中位线定理可知OD∥AB1 , 故而AB1∥平面BC1D;(2)把△BCD看做棱锥的底面,则棱锥的高为CC1 , 代入体积公式计算即可.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中,B1C与对角面DD1B1B所成角的大小是( )
A.15°
B.30°
C.45°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
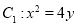 的焦点
的焦点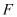 也是椭圆
也是椭圆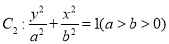 的一个焦点,
的一个焦点, 与
与 的公共弦的长为
的公共弦的长为 .
.(1)求
 的方程;
的方程;(2)过点
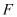 的直线
的直线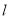 与
与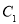 相交于
相交于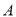 ,
,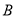 两点,与
两点,与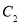 相交于
相交于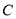 ,
,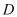 两点,且
两点,且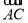 与
与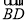 同向
同向(ⅰ)若
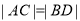 ,求直线
,求直线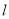 的斜率
的斜率(ⅱ)设
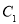 在点
在点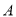 处的切线与
处的切线与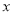 轴的交点为
轴的交点为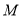 ,证明:直线
,证明:直线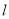 绕点
绕点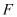 旋转时,
旋转时,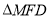 总是钝角三角形
总是钝角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是:
①三角形;②矩形;③正方形;④正六边形.
其中正确的结论是(把你认为正确的序号都填上) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=kx+b的图象过点(2,1),且b2﹣6b+9≤0
(1)求函数f(x)的解析式;
(2)若a>0,解关于x的不等式x2﹣(a2+a+1)x+a3+3<f(x). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
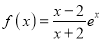 ,
, 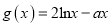 (
(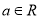 )
)(Ⅰ)讨论
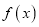 的单调性;
的单调性;(Ⅱ)证明:当
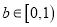 时,函数
时,函数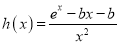 (
(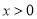 )有最小值.记
)有最小值.记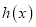 的最小值为
的最小值为 ,求
,求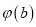 的值域;
的值域;(Ⅲ)若
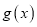 存在两个不同的零点
存在两个不同的零点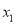 ,
, 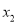 (
(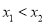 ),求
),求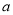 的取值范围,并比较
的取值范围,并比较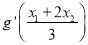 与0的大小.
与0的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=3,AC边上的中线BD=
 ,
, 
 =5.
=5.
(1)求AC的长;
(2)求sin(2A﹣B)的值.
相关试题

