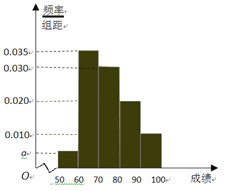
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?
参考答案:
【答案】(1)![]() ;(2)74.5;(3)
;(2)74.5;(3)![]()
【解析】试题分析:(1)根据频率分布直方图性质,每个小长方形面积等于该组的频率,所有小长方形面积和等于![]() ,所以
,所以![]() ,可以求出
,可以求出![]() ;(2)本问考查由频率分布直方图估算样本数据的平均数,用每组的频率乘以该组数据中点横坐标的值,再相加即可;(3)根据频率分布直方图可知,第三、四、五组的频率之比为
;(2)本问考查由频率分布直方图估算样本数据的平均数,用每组的频率乘以该组数据中点横坐标的值,再相加即可;(3)根据频率分布直方图可知,第三、四、五组的频率之比为![]() ,根据分层抽样性质,第三、四、五组抽取人数一次为
,根据分层抽样性质,第三、四、五组抽取人数一次为![]() 人,
人, ![]() 人,
人, ![]() 人,从
人,从![]() 人随机抽取
人随机抽取![]() 人,共有
人,共有![]() 种不同的抽取方法,再求出恰有
种不同的抽取方法,再求出恰有![]() 人不低于
人不低于![]() 分的事件个数,就可以求出相应的概率.
分的事件个数,就可以求出相应的概率.
试题解析:(1)由题意得![]() ,所以
,所以![]() ;
;
(2)由直方图分数在![]() 的频率为0.05,
的频率为0.05, ![]() 的频率为0.35,
的频率为0.35, ![]() 的频率为0.30,
的频率为0.30, ![]() 的频率为0.20,
的频率为0.20, ![]() 的频率为0.10,所以这100名学生期中考试数学成绩的平均分的估计值为:
的频率为0.10,所以这100名学生期中考试数学成绩的平均分的估计值为:
![]() ;
;
(3)由直方图,得:第3组人数为: ![]() 人,
人,
第4组人数为: ![]() 人,
人,
第5组人数为: ![]() 人,
人,
所以利用分层抽样在60名学生中抽取6名学生,
每组分别为:第3组: ![]() 人,
人,
第4组: ![]() 人,
人,
第5组: ![]() 人,
人,
所以第3、4、5组分别抽取3人、2人、1人.
设第3组的3位同学为![]() ,第4组的2位同学为
,第4组的2位同学为![]() ,第5组的1位同学为
,第5组的1位同学为![]() ,则从六位同学中抽两位同学有15种可能如下:
,则从六位同学中抽两位同学有15种可能如下:
![]() ,
,
![]() ,
,
其中恰有1人的分数不低于90分的情形有: ![]() ,共5种,所以其中第4组的2位同学至少有一位同学入选的概率为
,共5种,所以其中第4组的2位同学至少有一位同学入选的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
 ,解不等式
,解不等式 ;
;(2)若存在实数
 ,使得不等式
,使得不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2016~2017·郑州高一检测)过点M(1,2)的直线l与圆C:(x-3)2+(y-4)2=25交于A,B两点,C为圆心,当∠ACB最小时,直线l的方程是 ( )
A. x-2y+3=0 B. 2x+y-4=0
C. x-y+1=0 D. x+y-3=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题12分)甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5项预赛成绩记录如下:
甲
82
82
79
95
87
乙
95
75
80
90
85
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.
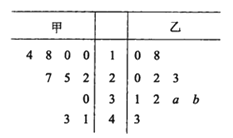
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)当
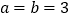 时,记甲型号电视机的“星级卖场”数量为
时,记甲型号电视机的“星级卖场”数量为 ,乙型号电视机的“星级卖场”数量为
,乙型号电视机的“星级卖场”数量为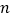 ,比较
,比较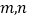 的大小关系;
的大小关系;(2)在这10个卖场中,随机选取2个卖场,记
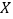 为其中甲型号电视机的“星级卖场”的个数,求
为其中甲型号电视机的“星级卖场”的个数,求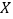 的分布列和数学期望;
的分布列和数学期望;(3)若
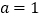 ,记乙型号电视机销售量的方差为
,记乙型号电视机销售量的方差为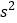 ,根据茎叶图推断
,根据茎叶图推断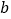 为何值时,
为何值时,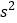 达到最小值.(只需写出结论)
达到最小值.(只需写出结论) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=2sin(x-
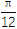 )-
)-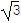 ,现将f(x)的图象向左平移
,现将f(x)的图象向左平移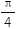 个单位长度,再向上平移
个单位长度,再向上平移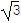 个单位长度,得到函数g(x)的图象.
个单位长度,得到函数g(x)的图象.(1)求f(
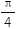 )+g(
)+g(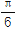 )的值;
)的值;(2)若a,b,c分别是△ABC三个内角A,B,C的对边,a+c=4,且当x=B时,g(x)取得最大值,求b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
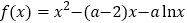 .
.(1)求函数
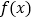 的单调区间;
的单调区间;(2)若函数
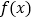 有两个零点,求满足条件的最小正整数
有两个零点,求满足条件的最小正整数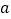 的值;
的值;(3)若方程
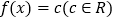 ,有两个不相等的实数根
,有两个不相等的实数根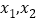 ,比较
,比较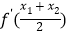 与0的大小.
与0的大小.
相关试题

