【题目】设函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 有两个零点,求满足条件的最小正整数
有两个零点,求满足条件的最小正整数![]() 的值;
的值;
(3)若方程![]() ,有两个不相等的实数根
,有两个不相等的实数根![]() ,比较
,比较![]() 与0的大小.
与0的大小.
参考答案:
【答案】(1) 单调增区间为![]() ,单调减区间为
,单调减区间为![]() . (2)
. (2) ![]() ,(3)详见解析
,(3)详见解析
【解析】试题分析: (1)先求函数导数,再求导函数零点![]() ,根据定义域舍去
,根据定义域舍去![]() ,对
,对![]() 进行讨论,
进行讨论, ![]() 时,
时,![]() ,单调增区间为
,单调增区间为![]() .
.![]() 时,有增有减;(2) 函数
时,有增有减;(2) 函数![]() 有两个零点,所以函数必不单调,且最小值小于零 ,转化研究最小值为负的条件:
有两个零点,所以函数必不单调,且最小值小于零 ,转化研究最小值为负的条件:![]() ,由于此函数单调递增,所以只需利用零点存在定理探求即可,即取两个相邻整数点代入研究即可得
,由于此函数单调递增,所以只需利用零点存在定理探求即可,即取两个相邻整数点代入研究即可得![]() 的取值范围,进而确定整数值,(3)根据
的取值范围,进而确定整数值,(3)根据![]() ,所以只需判定
,所以只需判定![]() 大小,由
大小,由![]() 可解得
可解得![]() ,代入分析只需比较
,代入分析只需比较![]() 大小, 设
大小, 设![]() ,构造函数
,构造函数![]() ,利用导数可得最值,即可判定大小.
,利用导数可得最值,即可判定大小.
试题解析:(1)解:![]()
![]()
![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增,函数
上单调递增,函数![]() 的单调增区间为
的单调增区间为![]() .
.
当![]() 时,由
时,由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() .
.
所以函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(2)解:由(1)得,若函数![]() 有两个零点
有两个零点
则![]() ,且
,且![]() 的最小值
的最小值![]() ,即
,即![]() .
.
因为![]() ,所以
,所以![]() .令
.令![]() ,显然
,显然![]() 在
在![]() 上为增函数,
上为增函数,
且![]() ,
,![]() ,所以存在
,所以存在![]() ,
,![]() .
.
当![]() 时,
时,![]() ;当
;当时,
![]() .所以满足条件的最小正整数
.所以满足条件的最小正整数![]()
(3)证明:因为![]() 是方程
是方程![]() 的两个不等实根,由(1)知
的两个不等实根,由(1)知![]() .
.
不妨设![]() ,则
,则![]() ,
,![]() .
.
两式相减得![]() ,
,
即![]() .
.
所以![]() .因为
.因为![]() ,
,
当![]() 时,
时,![]() , 当x∈
, 当x∈![]() 时,
时,![]() ,
,
故只要证![]() 即可,即证明
即可,即证明![]() ,
,
即证明![]() ,
,
即证明![]() .设
.设![]() .
.
令![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() ,当且仅当t=1时,
,当且仅当t=1时,![]() ,所以
,所以![]() 在
在![]() 上是增函数.
上是增函数.
又![]() ,所以当
,所以当![]() 时,
时,![]() 总成立.所以原题得证
总成立.所以原题得证
-
科目: 来源: 题型:
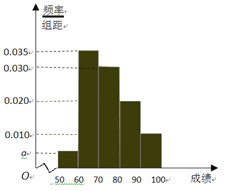
查看答案和解析>>【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号
第一组
第二组
第三组
第四组
第五组
分组
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.
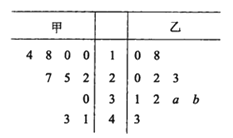
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)当
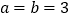 时,记甲型号电视机的“星级卖场”数量为
时,记甲型号电视机的“星级卖场”数量为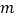 ,乙型号电视机的“星级卖场”数量为
,乙型号电视机的“星级卖场”数量为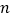 ,比较
,比较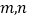 的大小关系;
的大小关系;(2)在这10个卖场中,随机选取2个卖场,记
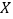 为其中甲型号电视机的“星级卖场”的个数,求
为其中甲型号电视机的“星级卖场”的个数,求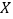 的分布列和数学期望;
的分布列和数学期望;(3)若
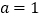 ,记乙型号电视机销售量的方差为
,记乙型号电视机销售量的方差为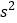 ,根据茎叶图推断
,根据茎叶图推断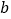 为何值时,
为何值时,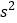 达到最小值.(只需写出结论)
达到最小值.(只需写出结论) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=2sin(x-
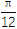 )-
)-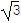 ,现将f(x)的图象向左平移
,现将f(x)的图象向左平移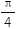 个单位长度,再向上平移
个单位长度,再向上平移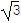 个单位长度,得到函数g(x)的图象.
个单位长度,得到函数g(x)的图象.(1)求f(
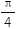 )+g(
)+g(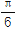 )的值;
)的值;(2)若a,b,c分别是△ABC三个内角A,B,C的对边,a+c=4,且当x=B时,g(x)取得最大值,求b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某小区准备将闲置的一直角三角形(其中∠B=
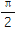 ,AB=a,BC=
,AB=a,BC=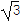 a)地块开发成公共绿地,设计时,要求绿地部分有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′落在边BC上,设∠AMN=θ.
a)地块开发成公共绿地,设计时,要求绿地部分有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′落在边BC上,设∠AMN=θ.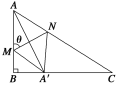
(1)若θ=
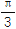 时,绿地“最美”,求最美绿地的面积;
时,绿地“最美”,求最美绿地的面积;(2)为方便小区居民的行走,设计时要求将AN,A′N的值设计最短,求此时绿地公共走道的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(1)求数列{bn}的通项公式;
(2)数列{bn}的前n项和为Sn,求证:数列
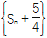 是等比数列.
是等比数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
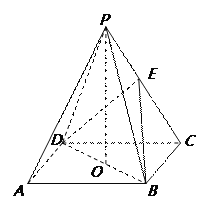
.求证:(Ⅰ)PA∥平面BDE;(Ⅱ)平面PAC⊥平面BDE;(III)若PB与底面所成的角为600, AB=2a,求三棱锥E-BCD的体积.
相关试题

