【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高 气温 | [10, 15) | [15, 20) | [20, 25) | [25, 30) | [30, 35) | [35, 40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列.
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)由题意知![]() 的可能取值为200,300,500,分别求出相应的概率,由此能求出
的可能取值为200,300,500,分别求出相应的概率,由此能求出![]() 的分布列.
的分布列.
(2)当![]() 时,
时, ![]() ,
, ![]() ;当
;当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .从而得到当
.从而得到当![]() 时,
时, ![]() 最大值为520元.
最大值为520元.
试题解析:(1)易知需求量可取200,300,500,
![]() ,
, ![]() ,
, ![]() ,
,
则分布列为:
|
|
|
|
|
|
|
|
(2)①当![]() 时,
时, ![]() ,此时
,此时![]() ,当
,当![]() 时取到;
时取到;
②当![]() 时,
时, ![]()
![]() ,
,
此时![]() ,当
,当![]() 时取到;
时取到;
③当![]() 时,
时,
![]()
![]() ,此时
,此时![]() ;④当
;④当![]() 时,易知一定小于③的情况.
时,易知一定小于③的情况.
综上所述,当![]() 时,取到最大值为520.
时,取到最大值为520.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知函数
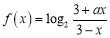 是函数值不恒为零的奇函数,函数
是函数值不恒为零的奇函数,函数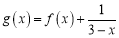 .
.(1)求实数
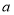 的值,并判断函数
的值,并判断函数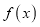 的单调性;
的单调性;(2)解关于
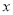 的不等式
的不等式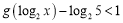 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
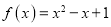 .
.(1)对于实数
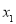 ,
,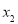 ,若
,若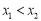 ,有
,有 ,求证:方程
,求证:方程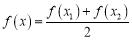 有两个不相等的实数根;
有两个不相等的实数根;(2)若
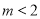 ,函数
,函数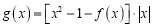 ,求函数
,求函数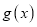 在区间
在区间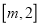 上的最大值和最小值;
上的最大值和最小值;(3)若存在实数
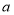 ,使得对于任意实数
,使得对于任意实数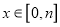 ,都有
,都有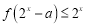 ,求实数
,求实数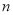 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】德国数学家科拉茨
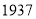 年提出了一个著名的猜想:任给一个正整数
年提出了一个著名的猜想:任给一个正整数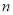 ,如果
,如果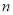 是偶数,就将它减半(即
是偶数,就将它减半(即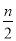 );如果
);如果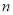 是奇数,则将它乘
是奇数,则将它乘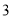 加
加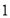 (即
(即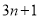 ),不断重复这样的运算,经过有限步后,一定可以得到
),不断重复这样的运算,经过有限步后,一定可以得到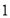 .对于科拉茨猜想,目前谁也不能证明,也不能否定.现在请你研究:如果对正整数
.对于科拉茨猜想,目前谁也不能证明,也不能否定.现在请你研究:如果对正整数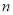 (首项)按照上述规则施行变换后的第
(首项)按照上述规则施行变换后的第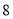 项为
项为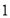 (注:
(注: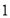 可以多次出现),则
可以多次出现),则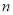 的所有不同值的个数为( )
的所有不同值的个数为( )A.
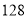 B.
B. 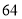 C.
C. 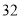 D.
D. 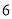
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知多面体
 的底面
的底面 是边长为
是边长为 的菱形,
的菱形, 
 底面
底面 ,
,  ,且
,且 .
.(1)证明:平面
 平面
平面 ;
;(2)若直线
 与平面
与平面 所成的角为
所成的角为 ,求二面角
,求二面角 的余弦值.
的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017高考新课标Ⅲ,理19)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.

(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体
 中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN∥平面EFDB.
中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN∥平面EFDB.
相关试题

