【题目】某精密仪器生产有两道相互独立的先后工序,每道工序都要经过相互独立的工序检查,且当第一道工序检查合格后才能进入第二道工序,两道工序都合格,产品才完全合格,.经长期监测发现,该仪器第一道工序检查合格的概率为 ![]() ,第二道工序检查合格的概率为
,第二道工序检查合格的概率为 ![]() ,已知该厂三个生产小组分别每月负责生产一台这种仪器.
,已知该厂三个生产小组分别每月负责生产一台这种仪器.
(1)求本月恰有两台仪器完全合格的概率;
(2)若生产一台仪器合格可盈利5万元,不合格则要亏损1万元,记该厂每月的赢利额为ξ,求ξ的分布列和每月的盈利期望.
参考答案:
【答案】
(1)解:设恰有两台仪器完全合格的事件为A,每台仪器经两道工序检验完全合格的概率为 ![]()
所以 ![]() …
…
(2)解:每月生产的仪器完全合格的台数可为3,2,1,0四种
所以赢利额ξ的数额可以为15,9,3,﹣3…(7分)
当ξ=15时, ![]()
当ξ=9时, ![]()
当ξ=3时, ![]()
当ξ=﹣3时, ![]()
每月的盈利期望 ![]()
所以每月的盈利期望值为10.14万元
【解析】(1)求出每生产一台合格仪器的概率,利用独立重复试验的概率公式求本月恰有两台仪器完全合格的概率;(2)根据题意得到变量的可能的取值,根据变量对应的事件,利用独立重复试验的概率公式得到概率,写出分布列,根据做出的变量的分布列,代入求期望值的公式做出期望值
【考点精析】解答此题的关键在于理解离散型随机变量及其分布列的相关知识,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市地铁全线共有四个车站,甲、乙两人同时在地铁第1号车站(首发站)乘车,假设每人自第2号站开始,在每个车站下车是等可能的,约定用有序实数对
 表示“甲在
表示“甲在 号车站下车,乙在
号车站下车,乙在 号车站下车”
号车站下车”(Ⅰ)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
(Ⅱ)求甲、乙两人同在第3号车站下车的概率;
(Ⅲ)求甲、乙两人在不同的车站下车的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是定义域
是定义域 上的单调递增函数
上的单调递增函数(1)求证:命题“设
 ,若
,若 ,则
,则 ”是真命题
”是真命题(2)解关于
 的不等式
的不等式
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 为常数.
为常数.(1)若
 ,求函数
,求函数 的极值;
的极值;(2)若函数
 在
在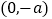 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为
 .
.
(1)求数列{an}的通项公式an;
(2)是否存在正整数n,使得 ?若存在,求出n值;若不存在,说明理由.
?若存在,求出n值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),在以原点为极点,
为参数),在以原点为极点,  轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线 的极坐标方程为
的极坐标方程为 .
.(1)求曲线
 的普通方程和直线
的普通方程和直线 的倾斜角;
的倾斜角;(2)设点
 ,直线
,直线 和曲线
和曲线 交于
交于 两点,求
两点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, 平面
平面 ,
, ,
,
 ,
, ,点Q在棱AB上.
,点Q在棱AB上.(1)证明:
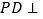 平面
平面 .
.(2)若三棱锥
 的体积为
的体积为 ,求点B到平面PDQ的距离.
,求点B到平面PDQ的距离.
相关试题

