【题目】已知某人做某件事,成功的概率只有0.1.用计算器计算,如果他尝试10次,而且每次是否成功都相互独立,则他至少有一次成功的概率为多少(精确到0.01)?如果他尝试20次呢?如果要保证至少成功一次的概率不小于90%,则他至少要尝试多少次?
参考答案:
【答案】见解析.
【解析】
根据相互独立事件的乘法公式以及对立事件的概率公式,借助计算器可得答案.
解:依题意,他尝试一次,不成功的概率为![]() ,由于每次是否成功都相互独立,所以他尝试10次,均不成功的概率为
,由于每次是否成功都相互独立,所以他尝试10次,均不成功的概率为![]() ,则至少有一次成功的概率
,则至少有一次成功的概率![]() .
.
同理,他尝试20次,至少有一次成功的概率为![]() .
.
设他尝试n次,才能保证至少成功一次的概卒不小于90%,则有![]() ,即
,即![]() ,解得
,解得![]() .故
.故![]() .
.
即他至少尝试22次,才能保证其至少成功一次的概率不小于90%.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 ,
, ,已知曲线
,已知曲线 与
与 在原点处的切线相同.
在原点处的切线相同.(1)求
 的单调区间;
的单调区间;(2)当
 时,
时,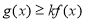 恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 有如下性质:如果常数
有如下性质:如果常数 ,那么该函数在
,那么该函数在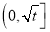 上是减函数,在
上是减函数,在 上是增函数.
上是增函数.(1)已知函数
 ,利用上述性质,求函数
,利用上述性质,求函数 的单调区间和值域;
的单调区间和值域;(2)已知函数
 =
= 和函数
和函数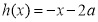 ,若对任意
,若对任意 ,总存在
,总存在 ,使得
,使得 (x2)=
(x2)= 成立,求实数
成立,求实数 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】俗话说“三个臭皮匠,顶个诸葛亮”,从数学角度解释这句话的含义.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂家具车间做A,B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A,B型桌子分别需要1小时和2小时,漆工油漆一张A,B型桌子分别需要3小时和1小时;又知木工和漆工每天工作分别不得超过8小时和9小时,设该厂每天做A,B型桌子分别为x张和y张.
(1)试列出x,y满足的关系式,并画出相应的平面区域;
(2)若工厂做一张A,B型桌子分别获得利润为2千元和3千元,那么怎样安排A,B型桌子生产的张数,可使得所得利润最大,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正项数列
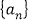 的前
的前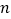 项和为
项和为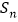 ,且
,且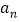 和
和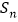 满足:
满足: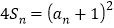
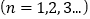 .
.(1)求
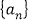 的通项公式;
的通项公式;(2)设
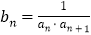 ,求
,求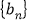 的前
的前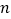 项和
项和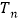 ;
;(3)在(2)的条件下,对任意
 ,
,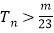 都成立,求整数
都成立,求整数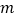 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,多面体
 中,
中, 为正方形,
为正方形, ,二面角
,二面角 的余弦值为
的余弦值为 ,且
,且 .
.(1)证明:平面
 平面
平面 ;
;(2)求平面
 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.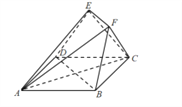
相关试题

