【题目】函数![]() ,
,![]() ,已知曲线
,已知曲线![]() 与
与![]() 在原点处的切线相同.
在原点处的切线相同.
(1)求![]() 的单调区间;
的单调区间;
(2)当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)借助条件确定![]() 的表达式,然后求导,解不等式得单调区间;(2)构建新函数,借助最值建立关于
的表达式,然后求导,解不等式得单调区间;(2)构建新函数,借助最值建立关于![]() 的不等关系.
的不等关系.
试题解析:解:(1)∵![]() (
(![]() ),
),![]() ,
,
依题意,![]() ,解得
,解得![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
故![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(2)令![]() ,
,
由(1)知:![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() .
.
(i)若![]() ,则
,则![]()
∴![]() 在
在![]() 上是增函数,
上是增函数,
∴![]() ,
,
∴![]() 成立.
成立.
(ii)若![]() ,由(1)知
,由(1)知![]() ,则
,则![]() ,
,
由(i)知:![]() ,
,
∴![]() 成立.
成立.
(iii)若![]() ,则
,则![]() ,则
,则![]() ,
,
显然![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,![]() ,
,
∴![]() 在
在![]() 上存在唯一零点
上存在唯一零点![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
从而![]() ,即
,即![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,
从而当![]() 时,
时,![]() ,即
,即![]() ,不合题意.
,不合题意.
综上,实数![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量
 与尺寸
与尺寸 之间近似满足关系式
之间近似满足关系式 为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间
为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间 内时为优等品.现随机抽取6件合格产品,测得数据如下:
内时为优等品.现随机抽取6件合格产品,测得数据如下:尺寸

38
48
58
68
78
88
质量

16.8
18.8
20.7
22.4
24
25.5
质量与尺寸的比

0.442
0.392
0.357
0.329
0.308
0.290
(Ⅰ)现从抽取的6件合格产品中再任选3件,求恰好取到2件优等品的概率;
(Ⅱ)根据测得数据作了初步处理,得相关统计量的值如下表:
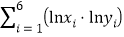



75.3
24.6
18.3
101.4
(i)根据所给统计量,求
 关于
关于 的回归方程;
的回归方程;(ii)已知优等品的收益
 (单位:千元)与
(单位:千元)与 的关系
的关系 ,则当优等品的尺寸为
,则当优等品的尺寸为 为何值时,收益
为何值时,收益 的预报值最大?(精确到0.1)
的预报值最大?(精确到0.1)附:对于样本
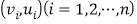 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
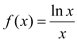 ,
, .
.(I)求函数
 的最大值;
的最大值;(II)当
 时,函数
时,函数 有最小值,记
有最小值,记 的最小值为
的最小值为 ,求函数
,求函数 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]上任取的一个实数,b是从区间[0,2]上任取的一个实数,求上述方程有实根的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 有如下性质:如果常数
有如下性质:如果常数 ,那么该函数在
,那么该函数在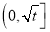 上是减函数,在
上是减函数,在 上是增函数.
上是增函数.(1)已知函数
 ,利用上述性质,求函数
,利用上述性质,求函数 的单调区间和值域;
的单调区间和值域;(2)已知函数
 =
= 和函数
和函数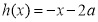 ,若对任意
,若对任意 ,总存在
,总存在 ,使得
,使得 (x2)=
(x2)= 成立,求实数
成立,求实数 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】俗话说“三个臭皮匠,顶个诸葛亮”,从数学角度解释这句话的含义.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某人做某件事,成功的概率只有0.1.用计算器计算,如果他尝试10次,而且每次是否成功都相互独立,则他至少有一次成功的概率为多少(精确到0.01)?如果他尝试20次呢?如果要保证至少成功一次的概率不小于90%,则他至少要尝试多少次?
相关试题

