【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:

(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|
参考答案:
【答案】(1)第二种生产方式的效率更高. 理由见解析
(2)80
(3)能
【解析】分析:(1)计算两种生产方式的平均时间即可。
(2)计算出中位数,再由茎叶图数据完成列联表。
(3)由公式计算出![]() ,再与6.635比较可得结果。
,再与6.635比较可得结果。
详解:(1)第二种生产方式的效率更高.
理由如下:
(i)由茎叶图可知:用第一种生产方式的工人中,有75%的工人完成生产任务所需时间至少80分钟,用第二种生产方式的工人中,有75%的工人完成生产任务所需时间至多79分钟.因此第二种生产方式的效率更高.
(ii)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间的中位数为85.5分钟,用第二种生产方式的工人完成生产任务所需时间的中位数为73.5分钟.因此第二种生产方式的效率更高.
(iii)由茎叶图可知:用第一种生产方式的工人完成生产任务平均所需时间高于80分钟;用第二种生产方式的工人完成生产任务平均所需时间低于80分钟,因此第二种生产方式的效率更高.
(iv)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间分布在茎8上的最多,关于茎8大致呈对称分布;用第二种生产方式的工人完成生产任务所需时间分布在茎7上的最多,关于茎7大致呈对称分布,又用两种生产方式的工人完成生产任务所需时间分布的区间相同,故可以认为用第二种生产方式完成生产任务所需的时间比用第一种生产方式完成生产任务所需的时间更少,因此第二种生产方式的效率更高.学科*网
以上给出了4种理由,考生答出其中任意一种或其他合理理由均可得分.
(2)由茎叶图知![]() .
.
列联表如下:
超过 | 不超过 | |
第一种生产方式 | 15 | 5 |
第二种生产方式 | 5 | 15 |
(3)由于![]() ,所以有99%的把握认为两种生产方式的效率有差异.
,所以有99%的把握认为两种生产方式的效率有差异.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求经过直线L1:3x + 4y – 5 = 0与直线L2:2x – 3y + 8 = 0的交点M,且满足下列条件的直线方程
(1)与直线2x + y + 5 = 0平行 ;
(2)与直线2x + y + 5 = 0垂直;
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
直线
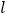 的参数方程为
的参数方程为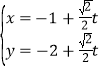 (
( 为参数),以坐标原点
为参数),以坐标原点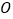 为极点,
为极点,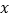 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线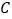 的极坐标方程为
的极坐标方程为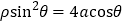 ,直线
,直线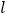 与曲线
与曲线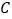 交于不同的两点
交于不同的两点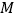 ,
,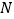 .
.(1)求实数
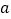 的取值范围;
的取值范围;(2)已知
 ,设点
,设点 ,若
,若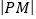 ,
,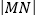 ,
,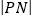 成等比数列,求
成等比数列,求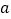 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3+ax2+bx+c,x∈[-2,2]表示过原点的曲线,且在x=±1处的切线的倾斜角均为
 π,有以下命题:
π,有以下命题:①f(x)的解析式为f(x)=x3-4x,x∈[-2,2].
②f(x)的极值点有且只有一个.
③f(x)的最大值与最小值之和等于零.
其中正确命题的序号为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax(lnx﹣1)﹣x2(a∈R)恰有两个极值点x1 , x2 , 且x1<x2 . (Ⅰ)求实数a的取值范围;
(Ⅱ)若不等式lnx1+λlnx2>1+λ恒成立,求实数λ的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在极坐标系中,点 P的极坐标是
 ,曲线 C的极坐标方程为
,曲线 C的极坐标方程为  .以极点为坐标原点,极轴为 x轴的正半轴建立平面直角坐标系,斜率为﹣1的直线 l经过点P.
.以极点为坐标原点,极轴为 x轴的正半轴建立平面直角坐标系,斜率为﹣1的直线 l经过点P.
(1)写出直线 l的参数方程和曲线 C的直角坐标方程;
(2)若直线 l和曲线C相交于两点A,B,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+2aln x.
(1)当a=1时,求函数f′(x)的最小值;
(2)求函数f(x)的单调区间和极值.
相关试题

