某租赁公司拥有汽车100辆.当每辆车的月租金为3 000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3 600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
参考答案:
解 (1)当每辆车的月租金为3 600元时,未租出的车辆数为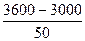 =12,
=12,
所以这时租出了88辆车.
(2)设每辆车的月租金定为x元,则租赁公司的月收益为
f(x)=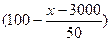 (x-150)-
(x-150)-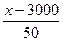 ×50,
×50,
整理得f(x)=-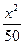 +162x-21 000=-
+162x-21 000=-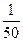 (x-4 050)2+307 050.
(x-4 050)2+307 050.
∴当x=4 050时,f(x)最大,最大值为f(4 050)=307 050.
答 (1)当每辆车的月租金定为3 600元时,能租出88辆车;
(2)当每辆车的月租金定为4 050元时,租赁公司的月收益最大,最大收益为307 050元
解析
-
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数
(1)当0≤x≤200时,求函数v(x)的表达式
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到1辆/小时) -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)已知函数
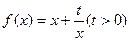 和点
和点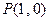 ,过点
,过点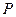 作曲线
作曲线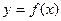 的两条切线
的两条切线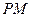 、
、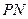 ,切点分别为
,切点分别为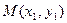 、
、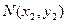 .
.
(1)求证: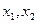 为关于
为关于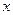 的方程
的方程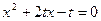 的两根;
的两根;
(2)设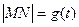 ,求函数
,求函数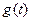 的表达式;
的表达式;
(3)在(2)的条件下,若在区间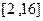 内总存在
内总存在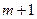 个实数
个实数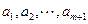 (可以相同),使得不等式
(可以相同),使得不等式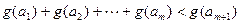 成立,求
成立,求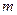 的最大值.
的最大值. -
科目: 来源: 题型:解答题
查看答案和解析>>提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情
 况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:
况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明: 当20≤x≤200时,车流速度v是车流密度x的一次函数.当0≤x≤200时,求函数v(x)的表达式.
当20≤x≤200时,车流速度v是车流密度x的一次函数.当0≤x≤200时,求函数v(x)的表达式. -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)已知函数f(x)=2x-
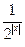 .
.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围. -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分15分)已知二次函数
 对
对 都满足
都满足 且
且 ,设函数
,设函数
( ,
, ).
).
(1)求 的表达式;
的表达式;
(2)若 ,使
,使
 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(3)设 ,
, ,求证:对于
,求证:对于 ,恒有
,恒有 .
. -
科目: 来源: 题型:解答题
查看答案和解析>>(本题11分)如图,矩形ABCD中,AB=6,BC=2
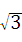 ,点O是AB的中点,点P在AB的延长线
,点O是AB的中点,点P在AB的延长线 上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点
上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点 出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积 为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;
为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;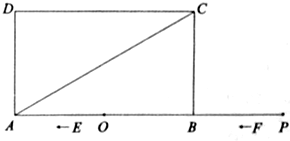
相关试题

