(本小题满分12分)已知函数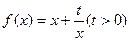 和点
和点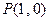 ,过点
,过点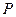 作曲线
作曲线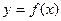 的两条切线
的两条切线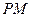 、
、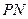 ,切点分别为
,切点分别为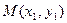 、
、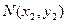 .
.
(1)求证: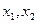 为关于
为关于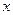 的方程
的方程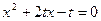 的两根;
的两根;
(2)设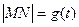 ,求函数
,求函数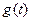 的表达式;
的表达式;
(3)在(2)的条件下,若在区间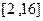 内总存在
内总存在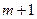 个实数
个实数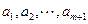 (可以相同),使得不等式
(可以相同),使得不等式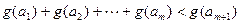 成立,求
成立,求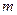 的最大值.
的最大值.
参考答案:
解:(1)由题意可知: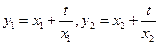
∵ 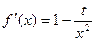 , ……………………………2分
, ……………………………2分
∴切线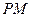 的方程为:
的方程为: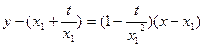 ,
,
又 切线
切线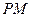 过点
过点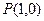 ,
, 有
有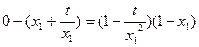 ,
,
即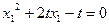 , ①
, ①
同理,由切线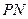 也过点
也过点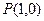 ,得
,得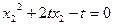 .②
.②
由①、②,可得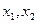 是方程
是方程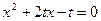 ( * )的两根……………………………4分
( * )的两根……………………………4分
(2)由( * )知.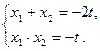
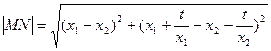
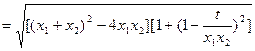
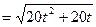 ,
,
∴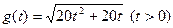 .……………………………8分
.……………………………8分
(3)易知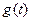 在区间
在区间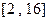 上为增函数,
上为增函数,
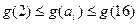
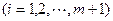 ,
,
则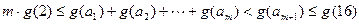 .……………………10分
.……………………10分
即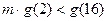 ,即
,即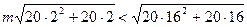 ,
,
所以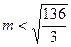 ,由于
,由于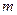 为正整数,所以
为正整数,所以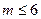 .
.
又当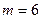 时,存在
时,存在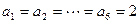 ,
,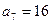 满足条件,
满足条件,
所以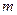 的最大值为
的最大值为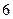 . …………12分
. …………12分
解析
-
科目: 来源: 题型:解答题
查看答案和解析>>(本题12分)已知不等式
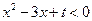 的解集为
的解集为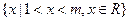 ;
;
(1)求 的值;
的值;
(2)若不等式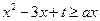 在
在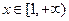 上恒成立,求实数
上恒成立,求实数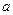 的最大值.
的最大值. -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)已知二次函数
 的图像经过坐
的图像经过坐 标原
标原 点,且满足
点,且满足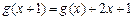 ,设函数
,设函数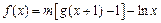 ,其中m为常数且
,其中m为常数且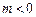 。
。
(1)求函数 的解析式;
的解析式;
(2)判断函数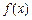 的单调性并说明理由。
的单调性并说明理由。 -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数
(1)当0≤x≤200时,求函数v(x)的表达式
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到1辆/小时) -
科目: 来源: 题型:解答题
查看答案和解析>>提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情
 况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:
况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明: 当20≤x≤200时,车流速度v是车流密度x的一次函数.当0≤x≤200时,求函数v(x)的表达式.
当20≤x≤200时,车流速度v是车流密度x的一次函数.当0≤x≤200时,求函数v(x)的表达式. -
科目: 来源: 题型:解答题
查看答案和解析>>某租赁公司拥有汽车100辆.当每辆车的月租金为3 000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3 600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少? -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)已知函数f(x)=2x-
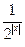 .
.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
相关试题

