搜索
【题目】设非零常数d是等差数列x1 ， x2 ， …，x19的公差，随机变量ξ等可能地取值x1 ， x2 ， …，x19 ， 则方差Dξ= ．
参考答案：
【答案】30d2
【解析】解：由题意可得Eξ= 
= 
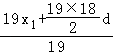=x1+9d．
∴xn﹣Eξ=x1+（n﹣1）d﹣（x1+9d）=（n﹣10）d，
∴Dξ= 
+…+（﹣d）2+0+d2+（2d）2+…+（9d）2]
= 
= 
=30d2 ．
所以答案是：30d2 ．
【考点精析】本题主要考查了极差、方差与标准差的相关知识点，需要掌握标准差和方差越大，数据的离散程度越大；标准差和方程为0时，样本各数据全相等，数据没有离散性；方差与原始数据单位不同，解决实际问题时，多采用标准差才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在边长为1的正六边形ABCDEF中，记以A为起点，其余顶点为终点的向量分别为
、 
、 
、 
、 
；以D为起点，其余顶点为终点的向量分别为 
、 
、 
、 
、 
．若m、M分别为（ 
+ 
+ 
）（ 
+ 
+ 
）的最小值、最大值，其中{i，j，k}{1，2，3，4，5}，{r，s，t}{1，2，3，4，5}，则m、M满足（ ）
A.m=0，M＞0
B.m＜0，M＞0
C.m＜0，M=0
D.m＜0，M＜0 -
科目： 来源： 题型：
查看答案和解析>>【题目】设抛物线的顶点在坐标原点，焦点F在
轴正半轴上，过点F的直线交抛物线于A,B两点，线段AB的长是8，AB的中点到
轴的距离是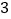
．(1)求抛物线的标准方程；
(2)在抛物线上是否存在不与原点重合的点P，使得过点P的直线交抛物线于另一点Q，满足
，且直线PQ与抛物线在点P处的切线垂直？并请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
（1）求
的定义域；（2）判断
的奇偶性并给予证明；（3）求关于x的不等式
的解集． -
科目： 来源： 题型：
查看答案和解析>>【题目】宝宝的健康成长是妈妈们最关心的问题，父母亲为婴儿选择什么品牌的奶粉一直以来都是育婴中的一个重要话题，为了解过程奶粉的知名度和消费者的信任度，某调查小组特别调查记录了某大型连锁超市2015年与2016年这两年销售量前5名的五个品牌奶粉的销量（单位：罐），绘制如下的管状图：
（1）根据给出的这两年销量的管状图，对该超市这两年品牌奶粉销量的前五强进行排名；
（2）分别计算这5个品牌奶粉2016年所占总销量（仅指这5个品牌奶粉的总销量）的百分比（百分数精确到各位），并将数据填入如下饼状图中的括号内；
（3）已知该超市2014年飞鹤奶粉的销量为
（单位：罐），试以
这3年的销量得出销量
关于
年份的线性回归方程，并据此预测2017年该超市飞鹤奶粉的销量.相关公式：
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知椭圆
，点B是其下顶点，过点B的直线交椭圆C于另一点A（A点在
轴下方），且线段AB的中点E在直线
上.
（1）求直线AB的方程；
（2）若点P为椭圆C上异于A、B的动点，且直线AP,BP分别交直线
于点M、N，证明：OM·ON为定值. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知
，
是两个单位向量，与，共面的向量
满足
，则
的最大值为（ ）A.
B. 2C. 
D. 1
相关试题
